Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Table Patterns Go Wild!



Table Patterns Go Wild! printable sheet
You might have made some times table patterns on hundred squares before. Some tables make vertical lines, some make diagonal lines and some make different patterns. Hundred squares are 10 by 10 grids, and in this problem we will call these '10 grids'.
Have a look at the 10 grids below.

Which times tables made these patterns? Why?
We are going to look at the patterns made on square grids of other sizes, from 4 grids (a 4 by 4 grid) to 9 grids.
These are patterns on a 7, a 5, an 8 and a 6 grid:
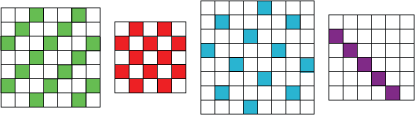
Which times tables made these patterns? Can you explain why they look like this?
Now it is time to do your own investigations. You can use grids drawn on squared paper or use this sheet of 10 grids.
Have a go at working out what makes vertical and diagonal lines on the different grids.
Can you make the checked pattern? What times table do you need to use on each grid?
Here are the top parts of some grids.
Can you identify which times table has been used to make each one?

Here are some parts of various grids. This time we have not shown the edges of the grids. Can you identify which times tables on which grids could have been used to make these patterns?

There may be more than one answer.

