Even and Odd
This activity is best done with a whole class or in a large group. Can you match the cards? What happens when you add pairs of the numbers together?
Problem
Even and Odd printable instruction sheet
Printable sets of cards: black cards, blue cards, green cards, red cards
This activity is best done as a whole class or in a large group.
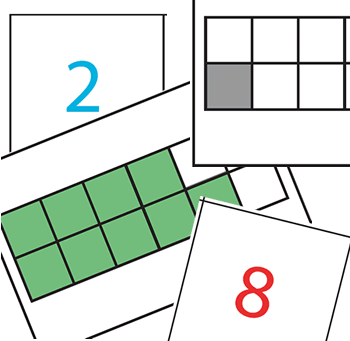
You will need to split up into four smaller groups: a black group, a blue group, a green group and a red group.
Each group will need the set of cards which has the same colour as their group name. These can be found at the top of this page, and they will need to be printed out and cut up into separate cards.
In your group, can you pair up your cards so that each number card goes with a card which has a picture of that same number of coloured squares?
Use interlocking cubes, such as Multilink, to make the numbers on your cards in the same way as the pictures of coloured squares. For example, here is the number 9 represented with Multilink cubes:
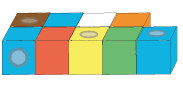
Nine is an odd number. Could you tell this from looking at the diagram of the block of cubes.Eight is an even number. How would the shape of the block of eight cubes differ?
Choose two of your numbers made from Multilink. What happens when you add them by fitting the two Multilink 'blocks' together? What kind of number do you get? Is it odd or even?
Choose a different pair of numbers and add them in the same way. What do you get this time? Is the number odd or even?
In your group, try this in as many different ways as you can.
You could record what you are doing in some way.
When do you get an odd number?
When do you get an even number?
Can you explain why?
Getting Started
If you don't have any interlocking cubes, you could shade squares on squared paper in the same way as the pictures of coloured squares. You could then cut out your 'blocks' of squares and choose two to fit together.
Student Solutions
This fun problem was about odd and even numbers; it also involved some counting, which is always a good thing! From this specific problem, some general rules began to emerge. This is very useful as these rules can be applied to other problems.
Matthew and Hannah from Stambridge submitted a lovely and clear solution:
Even numbers have two rows of the same number of blocks.
Odd numbers have one extra block in one of the rows.
When you add an odd number of blocks to an even number you get an odd number.
When you add an even number of blocks to an even number you get an even number.
When you add an odd number of blocks to an odd number you get an even number.
Class 4SK from Devonshire Primary also submitted a good solution:
E= Even and O= Odd
E+E=E
O+O=E
O+E=O
three odd numbers added = an odd number
They also explained why this is the case:
An odd number is a number with one left when we pair them up. So if we add two odd numbers, the two left over can make a pair.
Well done too to children from St Andrews CE Primary School in Oxford whose solution was very similar to Class 4SK's.
Thank you and well done to all those who submitted solutions! If you enjoyed this, why not try the following problem?
If you are only allowed to use 1s, 3s and 5s (but as many of each as you like), can you find all the ways to make 12 using four numbers? Can you find all the ways to make 13 using four numbers?
Teachers' Resources
Why do this problem?
This problem is designed to be worked on in groups so that lots of examples are generated. It offers opportunities for children to consolidate counting and addition, as well as giving them a way of 'seeing' odd and even numbers. The aim is for learners to be able to generalise the results of adding pairs of numbers together in terms of odds and evens.
Possible approach
This activity is best done with the whole class, split into four smaller groups. One group will need a copy of these black cards, one will need the blue cards, one the green cards and the fourth group will need the red cards.

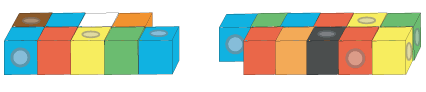
Draw the whole class together and ask one group to choose two of their Multilink numbers. Hold up the two blocks and ask how they could add them together. How many cubes would we have altogether? Invite children to come up and demonstrate. They may come up with different ways to join the two blocks so spend some time exploring this. Which way makes it easier to count the number of cubes? Listen out for explanations which focus on counting in twos, so it might be easiest to try to make blocks which are based on two 'rows' of Multilink. For example, adding 9 and 11:
Bring the children together again and explain that you have joined two blocks together to make a larger block as they have been doing. Show them a block of, for example, 15. What could the two smaller blocks have been? As children offer suggestions, draw representations of the numbers as squares, for example:
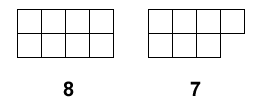
Gather several examples on the board and ask children what they notice. What is the same about all the examples? Listen out for observations about one of the numbers having a square 'sticking out' and one of the numbers forming a rectangular block which doesn't have a 'sticking out' square. If the children do not already know the vocabulary of odds and evens, then introduce this to them. What kind of number is 15? Encourage children to articulate that an odd number and an even number added together makes an odd number (or that an odd number can be made from one odd number and one even number added together).
Repeat this process with an even number, for example 12. What two numbers could have been added together to make 12? Gather examples on the board and encourage the generalisation in the same way: an odd number added to an odd number makes an even number, and an even number added to an even number makes an even number (or an even number can be made from two odd numbers added together or two even numbers added together).
Key questions
Possible extension
You could extend this challenge using a simplified version of Make 37: If you are only allowed to use 1s, 3s and 5s (but as many of each as you like), can you find all the ways to make 12 using four numbers? Can you find all the ways to make 13 using four numbers? This will allow you to assess whether they have fully understood the generalisation.
Possible support
If there are enough Multilink cubes, some children may find it easier to keep the models they make rather than making drawings on paper.
