Sort Them out (1)
Can you each work out the number on your card? What do you notice? How could you sort the cards?
Problem
Sort Them Out (1) printable sheet
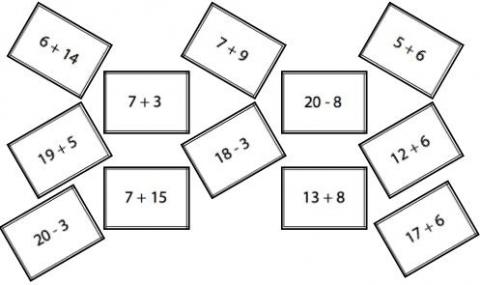
It's best to do this with $3$ other friends.
Share all the cards out equally among the four of you.
Work out what the answer is to each question on your cards.
Do you notice anything?
What do you notice?
Try sorting or arranging the cards in some way.
Getting Started
Remember that this activity is designed for you to try in a group so try to persuade some friends or family to join you!
You could check your calculations with someone else or by using a calculator.
Student Solutions
This problem provided a good opportunity to work with each other as a team. The cards gave you some practice with addition and subtraction, as well as challenging you to consider different ways of arranging them.
Courtenay and Emily from Ickford Combined School explained their method of sorting the cards:
We sorted the answers out in the two times table and the four times table and the ones that are in both times table and another group which is not in either the two and four times table.
Remember that all numbers in the four times table will feature in the two times table.
Caroline from Estes Hills Elementary, North Carolina, USA (Hello to the USA!) submitted her answer:
At first I sorted ten by itself and the teens together and the twentys together. Then I noticed that I could sort them by number order from $10$ to $24$.
Matthew from Stambridge looked at odd and even numbers:
First we separated the cards into additions and subtractions.
Next we looked at the answers.
In the addition pile we saw that:
E+E=E
O+O=E
E+O=O
O+E=O
In the subtraction pile we saw that:
E-O=O
O-E=O
O-O=E
E-E=E
So, you get an even answer from:
E-E
E+E
O+O
O-O
And so you get an odd answer from:
E-O
E+O
O-E
O+E
Can you think of other ways of arranging the cards?
Now have a go at Sort Them Out (2).
Teachers' Resources
Why do this problem?
The intention of this problem is that children will work together as a team. It should help in developing mathematical language as well as providing interesting practice in addition and subtraction and possibly offer opportunities to share calculation strategies. It gives ample opportunities to practise calculations using numbers to $20$ and should support children to remember these facts so that they are able to recall and use them whenever they need to do so.
Possible approach
The sheet of cards will need to be printed out. Give out a set of cards to each group of four to six children - it is important to give out all the cards in the set! (The questions asked in the set do vary in difficulty so you may like to choose who to give specific cards to.) To begin with, give children time to work individually on the questions on their own cards. After a suitable period of time, encourage them to ask each other about the questions and answers on other cards. At this stage, members of the group can help each other with the questions, but discourage them from simply giving someone else an answer.
Key questions
Possible extension
Possible support
You can purposely give certain cards to certain children if you do not want to take them too far out of their comfort zone where calculation is concerned. It may be appropriate for some learners to share cards with someone who is slightly more confident with addition and subtraction than they are themselves. Encourage them both to feel responsible for their findings and ensure everyone is involved in the class discussion.
