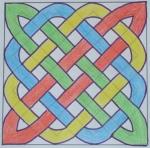
Drawing Celtic knots
Here is a chance to create some Celtic knots and explore the mathematics behind them.
Problem
Celtic knots are graphical representations of knots used for decoration by the ancient Celts. Here is a picture of an illuminated letter from a manuscript, showing intricate overlapping knots:
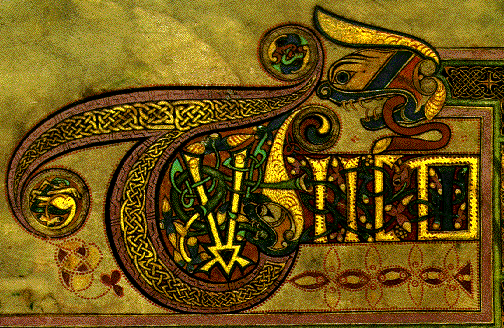
How about trying to draw some simple Celtic knots of your own? Watch the two videos, which show two different methods for drawing the same knot:
Alison's Video
Charlie's Video
Here are some images of completed knots. They have been coloured in so you can follow the different "ribbons" that make up the knot (click to enlarge):
You may find it useful to print off some of these grids (Word, pdf) to draw onto.
Alternatively, it is fairly simple to create your own grids by drawing faint diagonal lines on squared or square dotty paper. The straight lines needed to create the knots all go through the midpoints of the sides of the squares:

While you are drawing the Celtic knots, you may think of mathematical questions to ask.
Here are some questions that occured to us:
Try drawing some knots on square grids. What do you notice about the number of ribbons needed to create square knots? Can you explain your findings?
For rectangular knots, can you explain how the knot size determines the number of ribbons?
Is it possible to draw a rectangular Celtic knot without rotational symmetry?
Can you explain how the knot size determines the number of overlaps?
Send us your findings, and pictures of your knots.
Getting Started
Start with smaller grids.
Start by shading where the "ribbons" will go, and then draw in the knot systematically by drawing an over and under sequence.
Student Solutions
William from Barnton Community Primary School discovered that:
If there is a rectangular Celtic knot that is M by N then the number of ribbons is the highest common factor of M and N.
In this case M = 5 and N = 3 so the number of ribbons is 1.

Therefore, if a square Celtic knot has side length x, the number of different ribbons will be x.
In this case x = 4 so the number of ribbons is 4.

The number of crossovers for a square Celtic knot is $$2x^2 - 2x$$ or $$2x (x - 1)$$
Students from Garden International School also worked on this problem. Here is what Kenn, Jong Woong, Jayme and Marana sent us.
Teachers' Resources
Why do this problem?
The complexity in the seemingly simple patterns of Celtic knots have always fascinated people. This problem provides an accessible introduction to creating such patterns, with the chance to investigate some of the maths that arises along the way.
It could provide an excellent opportunity for forging cross-curricular links with Art and Design departments.
Possible approach
Learners could initially be shown images of Celtic knots to capture their interest. Then they could watch the videos to see two different ways of creating a basic knot.
Once they are ready to create their own knots, you may find it useful to print off some of these grids for learners to draw onto (Word, pdf).
Alternatively, it is fairly simple for learners to create their own grids by drawing faint diagonal lines on squared or square dotty paper. The straight lines needed to create the knots all go through the midpoints of the sides of the squares:

Once learners have got the hang of creating Celtic knots, encourage them to think of mathematical questions to ask - there are some suggestions in the problem. By getting everyone in the class to draw different knots, data can quickly be gathered and analysed. If learners have created their own grids, they may find that knots cannot be drawn on some grids - this is another line of enquiry that can be explored.
Key questions
For rectangular knots, can you explain how the knot size determines the number of ribbons?
Is it possible to draw a rectangular Celtic knot without rotational symmetry?
Can you explain how the knot size determines the number of overlaps?
Possible extension
Introduce learners to more complicated Celtic knots - circular knots, knots with holes in, letters drawn as knots...
Possible support
Starting on smaller grids and encouraging learners to shade in where the ribbons will go can help. Suggest they use soft pencil, and be prepared to do lots of rubbing out!