Rolling Triangle
Problem
The triangle ABC is equilateral. The arc AB has centre C , the arc BC has centre A , the arc CA has centre B and all three arcs have the same radius equal in length to the sides of the triangle.
Imagine a roller that has this cross-section. Place it on the floor and lay a plank of wood across it. Try to push the plank horizontally on the roller. What happens and why?
Though the animation shows the rolling triangle contained in a box, we are asking you to describe what happens when it rolls along the floor with a plank of wood on top of it..
Image
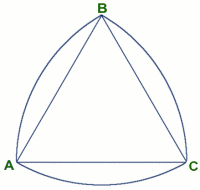
|
See also the Coke Machine problem. This relates to the 50 pence piece which is a seven sided rouleaux (rolling) figure, based on a regular septagon.
CHRISTMAS DECORATIONS
If you make lots of these rolling triangles from old greetings cards and score them along the edges of the equilateral triangles you can make the regular solids (a tetrahedron, an octahedron and an icosahedron) by sticking the flaps together. They look good with the flaps projecting outwards and they are easy to make. You can also make a dodecahedron using 12 rolling pentagons. A rolling pentagon is made in a similar way starting with a regular pentagon.

Getting Started
Notice what happens to the motion when the sides of the triangle are perpendicular to the floor and plank.
Notice the differences to what happens on the floor and on the plank when the triangle rolls in opposite directions.
You might like to try cutting out a very accurate rolling triangle with which to experiment.
Student Solutions
Brian sent us his thoughts on this problem:
What happens: It is impossible to tell from the motion of the plank that the roller is not circular. The plank moves forwards at a steady rate (assuming a steady push!) and remains at a constant height (the side length of the triangle) above the floor.

Why: Consider a starting point with C on the floor and the plank parallel to the floor and touching the roller at B (BC is vertical). Move the plank, rolling the roller, until the plank is touching the roller at A (so now AC is vertical). The roller will be rotating about C. Clearly, given that curve AB is equidistant from C, the plank will remain at a constant height above the floor. The same arguments can be used if a vertex is against the plank and the circular section is against the floor; only the frame of reference is changed and relative motion of plank and floor are the same.At the point of transition, both cases are simultaneously true.
Now consider the transition. In this example, C will be on the floor, A will be against the plank, and any further movement will result in A being effectively fixed on the plank and curve BC rolling on the floor. Note that the tangent to curve BC at C is parallel to the tangent to curve AB at A --- AC is a common radius of both curves. Hence at the transition there will be smooth transfer of movement from one mode to the other. Despite one's intuitive notions, the roller will therefore have a smooth forward motion!
