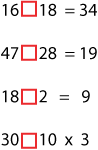Which Symbol?
Choose a symbol to put into the number sentence.
Problem
Use $+ , -, \times , \div$ and $=$ .
For example:
$2$ __ $3 = 6$
is
$2\times 3 = 6$
and
$3$ __ $5 - 2$
is
$3 = 5 - 2$
$16$ __ $18 = 34$
$47$ __ $28 = 19$
$18$ __ $2 = 9$
$30$ __ $10\times3$
All of the number sentences below, except two, have two solutions.
Can you find the symbols to use?
$51$ __ $36$ __ $15$
$45$ __ $5$ __ $9$
$27$ __ $36$ __ $63$
$70$ __ $14$ __ $56$
$7$ __ $5$ __ $35$
$50$ __ $5$ __ $10$
Which two number sentences have only one answer?
Can you see why?
Getting Started
It might help to have labelled counters with the five symbols $+ , -, \times , \div$ and $ =$ on them, which you can move around on this sheet.
Student Solutions
This problem challenged you to check your understanding of the building blocks of maths: "plus", "minus", "divide", and "multiply". You noticed that the order of numbers and symbols is important; in different positions, the "number sentence" can say different things. This is the same as when you speak or write; the order of the words matters. However, with some of the number sentences, there are two different orders, which still mean the same thing. Again, this is like speaking or writing; even if the order is different, it can sometimes mean the same thing.
For the first four questions, you were asked to put the correct symbol into the box. Several students submitted correct solutions. These include: Jonathan, Jordan, and Callum from Aycliffe Drive Primary School, Lauren from Princess Elizabeth, Anna, Isabella, George, Sophie, and Rhiannon from St. Swithun's, Nathan from Wilson's, Rebecca from Bourne Westfield primary school, Ayush from Garden Gate Elementary School, Brandon, Narissa, Jordan, Justin, and Cameron from Village Elementary, and Charlotte from Manor Preparatory School.
Narissa and Jordan wrote out the answer:
$16+18=34$
$47-28=19$
$18\div 2=9$
$30=10\times 3$
Rhiannon, from St Swithun's Primary School approached this problem by trial and improvement: she placed a different symbol in the box, and looked to see if the calculation made sense. In this way, she worked out the correct symbols.
The next part of the problem asked you to fill in the symbols, like in the first section. However, all of the number sentences but two have two different solutions. Ayush, from Garden Gate Elementary School submitted the correct solution:
$51- 36 = 15$
$51 = 36 + 15$
$45\div 5 = 9$
$45 = 5\times 9$
$27 + 36 = 63$
$70-14 = 56$
$70 = 14 + 56$
$7\times 5 = 35$
$50\div 5 = 10$
$50 = 5\times 10$
As Aimee, from Culford School points out:
The two sentences that only have one solution are:
$7\times 5=35$ and
$30=10\times3$
Rebecca, from Bourne Westfield Primary School explained:
On the $27+36=63$, the largest number is at the end so if you tried to make a second number sentence like $27=36-63$ it wouldn't give the right answer, because if you take away $63-36$ you would go into negative numbers. So, to get two "working" number sentences, you have to have the largest number at the front .
Here is an example to show a number sentence that works:
$50\div 5=10$ and $50=5\times 10$ .
This is a an example to show one that you can only do in one way: $7\times 5=35$.
Charlotte, from Manor Preparatory School, also submitted the correct solution.
A few people noticed a reason why there can be two different solutions for the number sentence. As Jonathan, Jordan and Callum, from Aycliffe Drive Primary School point out, "plus" and "minus" are inverse operations (processes), as are "multiply" and "divide". This means that you can do a sum, for example a multiplication, and then undo it, by doing the reverse, or "inverse": divide.
Thank you to everyone who submitted answers! Well done to you all!
Teachers' Resources
Why do this problem?
This problem is designed to help young learners to use the symbols plus, minus, multiplied by, divided by and equals to, meaningfully, in number statements. Children frequently meet boxes or similar devices to represent numbers but seldom the actual operational symbols. This problem also helps learners understand inverse operations.
Possible approach
Key questions
Possible extension
Learners could make some more number statements which can be done in more than one way. Can they make one that can be done three or even four ways?
Possible support
Suggest using counters with the five symbols on them which can be moved around on this sheet.