Kangaroo Subtraction
Can you solve this 'KANGAROO' alphanumeric subtraction?
Problem
In this subtraction, each of the letters K, A, N, G, R and O represents a different digit.
Image

What is the largest possible value of the number 'KAN'?
Student Solutions
Answer: KAN = 864 (and GAR = 765, OO = 99)
Using column subtraction
Image

A $-$ A = zero but O shouldn't be zero, so there must have been 'borrowing'/'regrouping'
Image
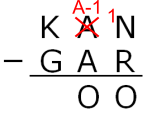
Image

In $^1$A-1, 1 is the tens digit
A-1 is the units digit
(10 + (A-1)) $-$ A = O so O = 9
Image

K$-$1 = G
$^1$N $-$ R = 9 means 10 + N $-$ R = 9 so R = N + 1
Largest possible KAN:
9 is taken so let K = 8 $\Rightarrow$ G = 7
A = 6
If N = 5 then R = 6 but 6 is taken
So N = 4 and R = 5
KAN = 864
Using algebra and logic
The difference between '$KAN$' and '$GAR$' is less than $100$ and since $K\neq G$ we must have $K=G+1$.
Next we must have $N < R$ else the difference between '$KAN$' and '$GAR$' would be at least $100$.
Let $R=N+x$ where $1< x< 9$. Then $OO=100-x$ and hence $O=9$ and $R=N+1$. Also we must have $K\leq 8$.
We want the largest value for $KAN$ so we try $K=8$. This forces $G=7$, hence must have $A\leq 6$. Set $A=6$, this forces $R\leq 5$ and hence $N\leq 4$ since $R=N+1$.
So $864$ is the largest possible value for $KAN$, and we have $864-765=99$.
