Inspect your gadgets
Chemistry is a highly investigative science. When a compound is synthesized and purified by an organic chemist, it is essential that the molecular structure (and 3D shape) of the compound is determined. These are qualities that affect the physical properties and reactivity of the molecule. Luckily chemists today have a vast array of spectroscopic "gadgets"- instruments which allow for a remarkably in depth structural assessment. In this article, we will cover some of the most useful of these techniques.
There are many possible methods by which structure may be elucidated by placing a chemical under a set of experimental circumstances and seeing the outcome, and is important to note which are the most useful and widely used in present day science. X-ray diffraction is the ultimate technique in terms of assigning structure to a molecule as it can be used to find the exact position of atoms in a molecule. However, this requires a single crystal of the pure compound and not all compounds can be crystallised in the required way, or structure in solution is required. Of the most widely used techniques, nuclear magnetic resonance (NMR) is by far the most important for a chemist as it uses the difference in the electronic environments of atoms to elucidate structure with good efficiency.
Mass spectrometry
Image


This tool works on the concept that ions can be separated according to their mass to charge ratio by application of electric and magnetic fields. Molecules are effectively weighed by this technique and they must be positively or negatively charged depending on the technique used. The plot generated by a typical mass spectrometer is of m/z ($\frac{\text{relative molecular mass}}{\text{relative charge}}$) against relative intensity.
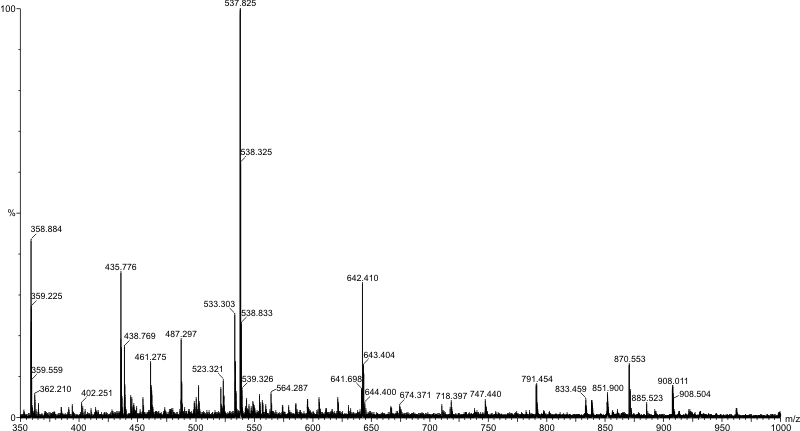
A single peak corresponding to the molecular ion, M$^+$, or pseudomolecular ion (the original molecule with an ion attached) in some cases, is not seen due to the fragmentation of the molecule within the instrument itself. The peak with the highest m/z value is usually the molecular ion (or pseudomolecular ion) but this is not always the case.
A mass spectrometer is a highly variable instrument but it does include 3 main components: an ion source, a mass analyser to separate the ions, and a detector. A high vacuum is used to avoid collisions between sample ions.
What would the difference be between a conventional mass spectrum and one conducted in an environment where there is no vacuum?
Ionization
The crudest technique is electron ionization (EI) where high energy electrons are fired and the sample vapour to generate positively charged molecular ions. The electrons removed are usually from lone pairs or multiple bonds (i.e. those that are less "core-like" and in higher energy orbitals. This method can cause large scale fragmentation. Chemical ionization (CI) techniques involve the use of a reagent gas in the ionization chamber (e.g. CH$_4$) at a partial pressure of 1000 times that of the sample. The reagent gas is more likely to be ionized and collisions between the ionized reagent and the sample can produce ions usually by some kind of proton transfer giving [M+H]$^+$. Fast atom bombardment (FAB) is useful for compounds which are hard to volatilize and involves bombardment of a matrix produced by mixing the sample with viscous glycerol by high energy atoms or ions of krypton or xenon. Ionization of large compounds such as proteins if facilitated by matrix assisted laser desorption (MALDI) which involves co-crystallization of the sample with an organic compound to give a matrix. This is then ionized by a laser set to a wavelength that is strongly absorbed by the organic compound.
The technique of choice for most labs in electrospray ionization. The sample is made up in solution with an added ionic compound such as a methoxide ion (MeO$^-$) and is sprayed to produce a fine aerosol which evaporate in the vacuum giving charged pseudomolecular ions. The advantages of this technique is that is is far more gentle and reduces the amount of fragmentation.
Mass separation
Early instruments used a series of magnetic and electric fields to deflect ions based on their mass and charge in an arc. More modern instruments use time of flight or quadrupole mass analyzers. These methods are quite simple to understand. The time of flight analyser accelerates packets of ions from the source to the same kinetic energy using an electric field.
What is the formula for kinetic energy of a particle? What can you say about the velocity of different fragments based on this relationship?
As ions drift into a field free region the different times that ions reach the detector give a measure of the m/z value of each fragment ion at this point.
Quadrupole mass analysis inolves altering the applied voltages to an arragement of 4 oppositely charged, equally polarised rods and an applied radio frequency (that causes the ion to accelerate in an alternating manner to and from the rods) to allow only ions of a desired mass : charge ratio to pass through the analyser. This works on the principle that unstable trajectories cause collisions with charged rods that neutralise the ions. Simultaneously altering the values of voltage and radio frequency separates ions according to m/z.
Another very interesting application of mass analysis is its use in tandem mass spectrometry, in which the first analyser allows the selection of an ion with a particular m/z value, the fragmentation of which can then be followed.
Detection
Electron multipliers are commonly used as detectors as they give a recordable electrical output. Array detectors may be used which detect ions with a range of masses simultaneously.
A well set up mass spectrometer is easily capable of measuring the mass of an ion to within 5 ppm or better. The value of a particular m/z peak is hugely improved due to this precision as using the atomic masses of specific isotopes, it makes it possible to determine the molecular formulae of ions through their exact masses. For example, consider a peak recorded at m/z = 30.0469. Potential candidates include:
$^{12}$C$_2$H$_6$ =
$^{15}$N$_2$ =
$^{14}$N$^{16}$O =
[$^{12}$C = 12 gmol$^{-1}$, $^{15}$N = 15.00011 gmol$^{-1}$, $^{14}$N = 14.00307 gmol$^{-1}$, $^{16}$O = 15.99491 gmol$^{-1}$, $^{1}$H = 1.00782 gmol$^{-1}$]
Calculate the relative molecular masses for each of these species using the accurate masses for each of the isotopes given. Which species corresponds to the peak?
Fragmentation
We spoke briefly about the usefulness of tandem mass spectroscopy earlier and the value of following the fragmentation of a specific ionic species. The fragmentation of a molecule is very useful as it gives information about the structure of the molecule (though there are better techniques available for structure determination).
The complexity of the fragmentation pattern means that it is highly specific to the compound. Mass spectroscopy is thus a useful tool in identifying compounds whose mass spectra have already been recorded. Often a molecule may show systematic fragmentation - for example peaks spaced at m/z 14 in long chain alkanes, corresponding to systematic losses of CH$_2$ groups. This is certainly useful in assigning each of the peaks to a specific ionic species. A tandem mass spectrum can be processed in such a way to show ions which fragmented to certain products which is useful in mixture analysis. The major advantage of mass spectroscopy is that the sample size for meaningful data is very small. However, the pattern of peaks is often more complex than expected and difficult to interpret.
Spectroscopy
The basis of all spectroscopy techniques is the quantisation of electron energy levels and the vibrational and rotational energy levels a molecule possesses. Promotion to another energy level can occur if a wavelength of light, corresponding to the difference in energy between two energy levels, is absorbed by a molecule ($\Delta$E = h$\upsilon$). The exact frequency of light absorbed is highly dependent on the particular molecule. DIfferent frequencies of light also cause different types of transition (again dependent on the difference in energy between two energy levels).
Nuclear magnetic resonance (NMR)

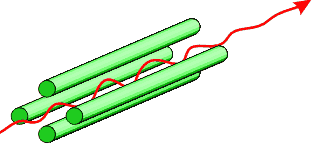
Nuclei can possess a spin and thus nuclei can have an associated weak magnetic field. In an applied magnetic field, an interaction with this spin gives rise to a set of nuclear spin energy levels. Absorption of radiowaves of the correct frequency facilitates a transition between energy levels that produces an NMR signal.
The nuclear spin quantum number, I, of a nucleus gives rise to (2I + 1) energy levels in an applied field. The value of I for a particular nucleus depends on the atomic number and the number of neutrons it contains. It may be taken as a guide that:
- nuclei with odd mass number have $\frac{1}{2}$ an integer spin value
- nuclei with odd atomic number and an odd number of neutrons have a spin value that is an integer
- nuclei with even atomic number and an even number of neutrons have 0 spin
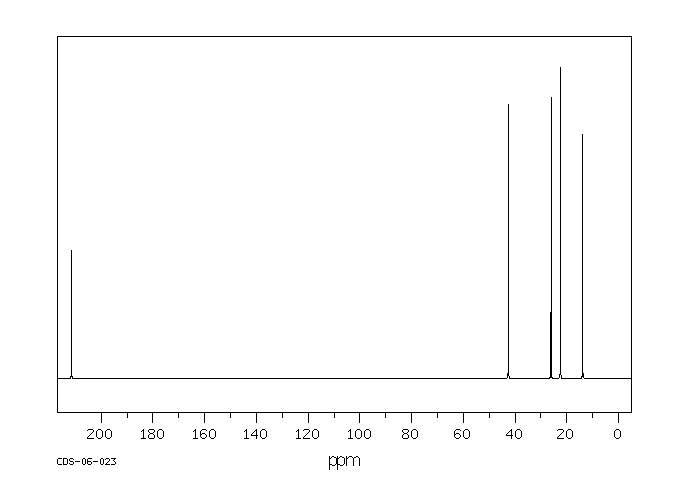
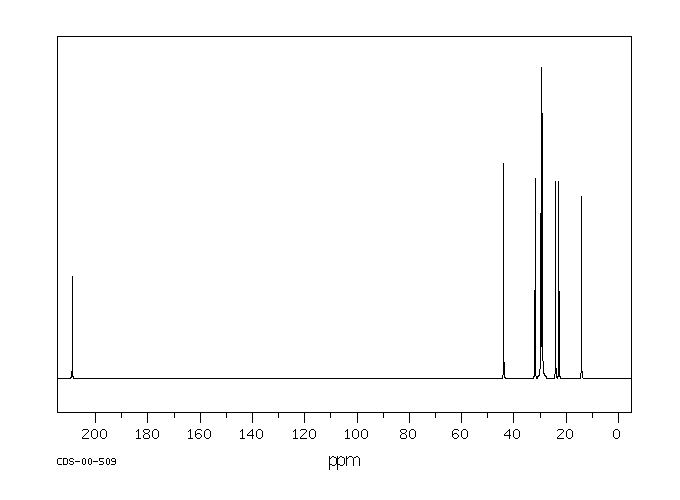
Can you draw the structures of 5-nonanone and 2-nonanone?
Given the above information, what would the $^13$C NMR spectrum of the following molecules look like? Draw in any lines of symmetry you see on the molecular structures.
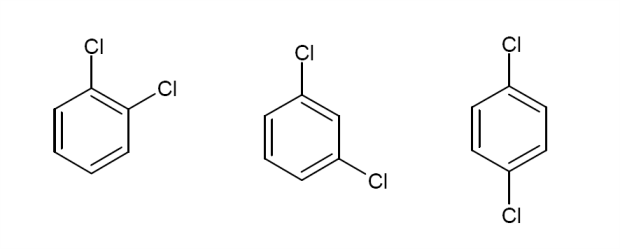
The NMR shift scale itself is established relative to the resonant frequency of a reference compound, meaning that any differences in the external magnetic field strength will affect all frequencies by the same factor. Thus the shift scale remain unaffected by any differences in effective magnetic field experienced by nuclei in a sample, whether this is due to the actual applied magnetic field or external variations, allowing for experimental comparison. TMS or tetramethylsilane is the reference compound of choice, being chemically inert, producing one signal in either $^13$C or $^1$H NMR that is far to the right of an observed spectrum.
$^{13}$C and $^{1}$H NMR
By far the most commonly used types of NMR are $^{13}$C and $^{1}$H NMR. Both of these nuclei have nuclear spin quantum number, I = $\frac{1}{2}$ and consequently possess 2 energy levels. Note that the resonant frequency of each nucleus in a certain magnetic field differs on the MHz level (c.f. environmental differences on the range of hundreds of Hz). For example in a 4.7 tesla magnetic field the resonant frequency of an $^{1}$H nucleus is 200 MHz whereas that of $^{13}$C is 50 MHz. Note that other types of high-field NMR spectroscopy are also possible including $^{19}$F and $^{31}$P NMR.
The advantage of $^{13}$C is its simplicity. There are usually fewer carbon environments in a molecule compared with hydrogen environments. The low natural abundance of $^{13}$C (1.1%) means that no C-C coupling is observed in a $^{13}$C NMR spectrum. $^{1}$H NMR is something you may already have encountered. $^{1}$H NMR gets very complicated due to the degree of coupling to many H atoms. This does have its advantages in elucidating more information about the structure of the molecule.
Coupling
Coupling is a very important phenomenon in NMR but what exactly is it and how does it come about?
We know that the frequency at which a nucleus resonates depends upon the local magnetic field it experiences. Coupling refers to a situation where a signal which would usually be a single peak is split about the original chemical shift position. The degree of separation gives the value of a coupling constant J, measured in Hz. The coupling constant is written $^x$J$_{\text{Y-Z}}$ where $x$ represents the number of bonds through which Z is coupling to a peak in a Y NMR spectrum.
In general, when a nucleus couples to $n$ equivalent nuclei with a certain spin value, $I$, its resonance signal is split into ($2nI + 1$) peaks. Coupling occurs due to the various spins of the coupling nucleus. Take for example a $^19$F nucleus of $I = \frac{1}{2}$. We know that the F nucleus thus has (2I + 1) = 2 energy levels. The separation between the 2 energy levels is so small that it is almost equally likely for a given $^19$F nucleus to be either spin up or spin down.
In the spin up state, the fluorine atom reinforces the magnetic field experience by the nucleus it is coupling to and shifts the resonant frequency to one slightly higher than the frequency the nucleus would normally resonate at.
What happens if the $^19$F nucleus is in the spin down state?
Coupling to 2 $^19$F nuclei gives a, ($2(2)(\frac{1}{2}) + 1$) = 3, triplet of peaks. This can be seen through a consideration of the possible spin states of fluorine.
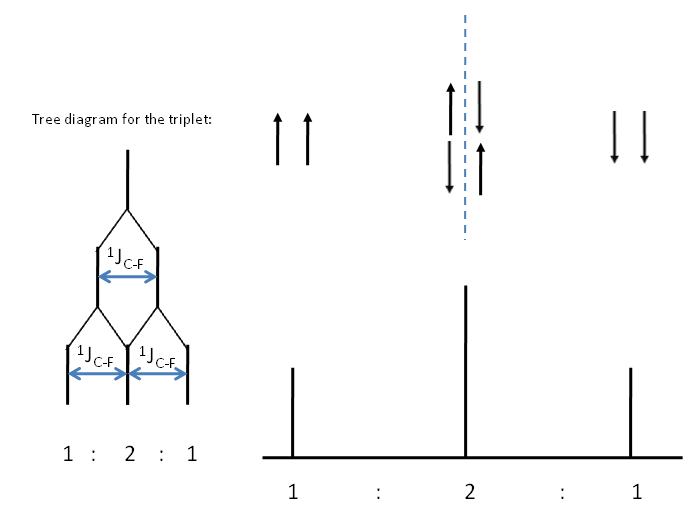
Consider the $^{13}$C spectrum of trifluoromethane.What possible combination of spin statescould the 3 fluorine atoms have? How many peaks is the $^{13}$C signal split into? Can you determine the relative intensity of these peaks?
You may be able to see the pattern with respect to $I = \frac{1}{2}$ nuclei gives a pattern of peak corresponding to the nth row of the Pascal's triangle. This can be reasoned in terms of combinatorics. Take for example the central peak of the spectrum representing coupling to 2 $^19$F nuclei. We have 2 nuclei of which one needs to be spin up and the other spin down. So $^2\textbf{C}_1$ = 2.
Of course coupling can be between different nuclei, in which case the relative values of the coupling constant $^x$J$_{\text{Y-Z}}$ requires consideration when sketching the shape of the NMR.
In terms of coupling it is important to note that:
- No C-H coupling is usually seen in $^{13}$C NMR as should be expected. This is because of decoupling. Broadband proton decoupling involves the irradiation of the sample over a large frequency range (to target all protons) in such a way that the nuclear spins of the $^1$H atoms oscillate so rapidly between spin "up" and "down" that their coupling contribution averages to 0.
- Splittings due to couplings between equivalent nuclei are not seen, though equivalent spins do interact with each other.
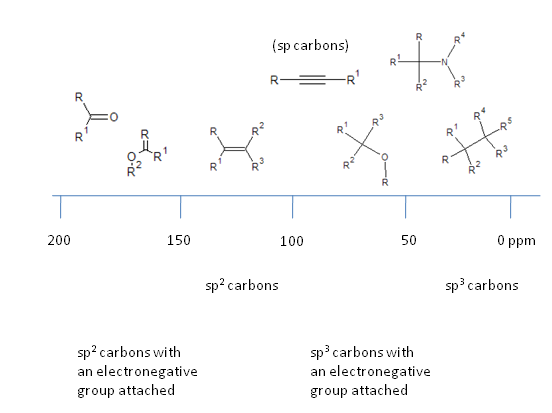
The NMR scale
Taking the $^{13}$C NMR spectrum as an example, the scale can be conveniently broken down. Note that electron withdrawing groups cause a deshielding of the nucleus in question, increasing the effective magnetic field it experiences and thus increases the energy separation and frequency at which the nucleus resonates.
Natural abundances
If there is coupling occurring due to a spin active species not present in large proportions in the sample, then satellite peaks are often seen. This is because for a proportion of the sample, coupling of the original signal occurs and splitting is seen, but for a significant proportion of the sample, no coupling is seen. Thus the original peak position contains a signal on the spectrum, superimposed with the splitting pattern due to the spin active proportion of the sample.
The relative intensities of these peaks are dictated by the terrestrial abundances of the coupling nucleus. Take for example the $^1$H NMR spectrum of chloroform as an example of this.
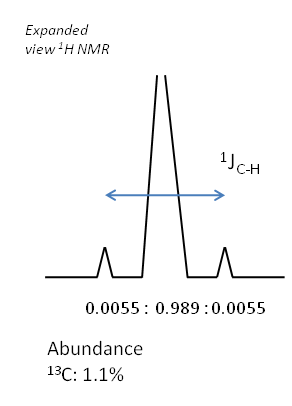
Consider the $^15$N NMR spectrum a molecule which contains a Pt-N bond and no other species bonded to the nitrogen that would make an impact on the splitting. The following isotopes of platinum exist in the following abundances:
$^{190}$Pt = 0.014%
$^{192}$Pt = 0.782%
$^{194}$Pt = 32.967%
$^{195}$Pt = 33.832%
$^{196}$Pt = 25.242%
$^{198}$Pt = 7.163%
Research the spin values of the following isotopes. What would the $^15$N NMR look like? What are the intensities of the observed peaks?
Infrared spectroscopy

IR spectroscopy works on the investigation of transition between vibrational energy levels in molecules. A typical IR plot describes the the percentage transmission across a range of wavelengths of applied infrared radiation. Absorption peaks thus correspond to downward pointing features. Frequency is given in wavenumbers where:
wavenumber, $\tilde\nu$ = $\frac{1}{\lambda}$
$\nu$ = $\frac{c}{\lambda}$
$\therefore\nu = c \times \tilde\nu$
Thus, $\nu$ $\alpha$ $\tilde\nu$
and as $\Delta E = h\nu$
hence $\Delta E$ $\alpha$ $\tilde\nu$
Large wavenumber values correspond to vibrational transitions which have a large associated energy change.
The harmonic oscillator is a useful model in this scenario and, mechanically, consists of a weight hanging from a spring whose displacement from an equilibrium position causes a restoring force to be generated. The weight therefore oscillates about an equilibrium position.
Hooke's law, $\nu$ $\alpha$ $\sqrt{\frac{k_f}{m}}$ where $\nu$ is the frequency of oscillation, ${k_f}$ is the force constant (difficulty of stretching in Nm$^{-1}$) and m is the mass, shows what the frequency of oscillation depends upon.
This model can be applied to a diatomic, modelled as two masses connected by a spring. It turns out there is a fair correlation between bond strength and the force constant. As there are now 2 masses involved we can take both into account by calculating the reduced mass of the system, $\mu$.
$\mu = \frac{m_1m_2}{m_1 + m_2}$ which has units of kg molecule$^{-1}$
Consider the situation where m_1 is far greater than m_2. What does the reduced mass simplify to?
The frequency of vibration for a diatomic is given by:
$\tilde\nu$ = $\frac{1}{2\pi c}\sqrt{\frac{k_f}{\mu}}$
So, the smaller $\mu$ becomes, the higher the frequency of oscillation. The higher the value of $k_f$ the higher the frequency of oscillation. Here is brief outline as to the division of a typical infrared spectrum.
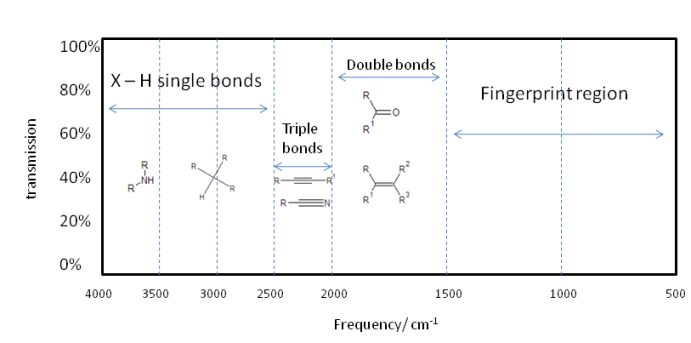
Of course the actual vibration of a molecule is far more complicated, but can be broken down to normal modes composed of cis and trans bends and various symmetric and asymmetric stretches. So a single absorption can correspond to many bond vibrations, but it is often a case that a given vibration largely corresponds to a certain part of a molecule vibrating. This allows for functional group identification which is very useful.
The larger the dipole of a vibrating bond the stronger the absorption so the larger the peak on the spectrum. This is because light interacts with the vibrating dipole because it is an oscillating electromagnetic field.
Can you classify the strength of absorption when the following bonds vibrate?
Symmetrical vibrations with no change in the dipole moment may be determined using a technique called Raman spectroscopy which analyses the scattering of light by vibrating bonds. Determining whether a given vibrational mode is IR active, Raman active or both is something beyond the scope of this article but we can say that:
- Homonuclear diatomics and heteronuclear diatomics are both Raman active.
- Homonuclear diatomics will clearly only be Raman active as they have no change in dipole moment on vibration.
For gaseous samples, a glass gas cell is filled. The windows of the cell through which IR passes are composed of cut and polished single crystal inorganic salts, not glass as this is an absorber of IR radiation. Salts have characteristic absorbances outside of the investigative range.
Liquid samples are applied as a thin film between sodium chloride plates. Thus liquid samples are quick and easy to analyse.
Solid samples can be prepared by grinding them up in a pestle and mortal witha viscuous hydrocarbon oil, nujol to make a mull that is sandwiched as a thin layer between sodium chloride plates. The solid may also be ground with dry KBr and the mix put into a mould and compressed in a hydraulic press. KBr exhibits cold flow under these conditions and the sample becomes incorporated into a transparent disk. The advantage of the latter method is it avoids the introduction of a hydrocarbon which typically absorbs over the investigative range.
Characteristic absorptions
Analysing an IR spectrum involves assigning absorption peaks to certain characteristic bond stretches. Bending vibrational modes are low frequency and found mainly in the fingerprint region- a useful area of the spectrum to give identity to samples that are one of a possible known range. Tables of typical absorbances are readily available and thus assignment of absorptions is an elementary task. Such analysis can often identify functional groups which means along with NMR, IR can prove a powerful complementary tool in structure determination.
We shall consider some of the more interesting examples in terms of absorption frequencies.
O-H absorption
O-H absorption peaks are typically broad due to the presence of hydrogen bonding within the sample. The strengths of O-H bonds vary slightly across the range of absorption frequencies. The peak is found at ~3200- 3600 cm$^{-1}$.
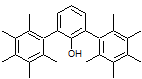
Consider the case of the above molecule. What would the the O-H absorption peak look like in this case? Give your reasoning, no matter how speculative it may be!
NO$_2$ group absorptions
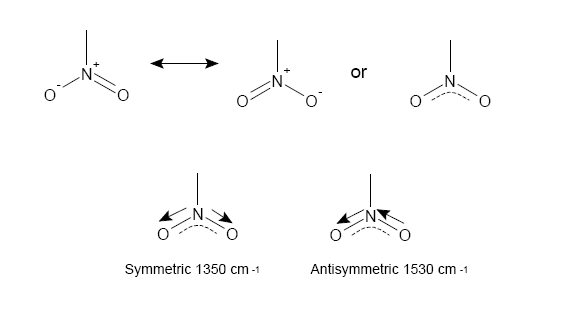
The NO$_2$ group has 2 stretches corresponding to a symmetric and antisymmetric bond stretch as seen above.
How easily is each stretch generated? Consider what this means about force constants and bonding considering our previous modelling.
Carbonyl groups
Patterns of absorption in the IR specturm for the C=O group are highly interesting as the exact frequency of the stretch can point to the sort of functional group present and can even give a guide to its chemical reactivity.
The ketone carbonyl gives a reference of the standard frequency of the C=O group as ~1715 cm$^{-1}$. As we saw previously an increase in bond strength corresponds broadly to an increase in $k_f$, meaning that a molecular environment can cause carbonyl absorption to rise to a higher frequency or lower frequency by respectively strengthening or weakening the carbonyl bond.
- Electron withdrawing carbonyl substituents strengthen the carbonyl as it increases the degree of polarity of the C=O bond increasing the electrostatic contribution to bond strength.
- Electron donating substituents weaken the carbonyl as donation occurs into the $\pi$* orbital, an orbital which has a large coefficient on the carbon atom causing a reduction in the polarity of the bond and also weakening the $\pi$ bond due to its antibonding nature.
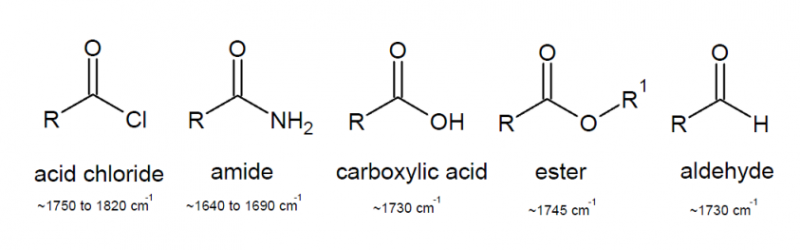
Of the above molecules, the acid chloride is generally the most reactive with the amide being the least reactive. If we consider that the mode of reaction at a carbonyl is generally by nucleophilic attack, it is easy to see why this is the case. The acid chloride with its highly polarised C=O bond makes the molecule a good electrophile. The $\delta ^+$ contribution on the carbon is increased by the inductive electron withdrawing effect of the Cl substituent, increasing its reactivity to nucleophiles. The lone pair on the N atom within the amide acts conjugatively, making the carbon less electrophilic by donation. This reduces the reactivity of the molecule and its ability to act as a good electrophile.
Conjugation and ring strain
The carbonyl bond is weakened by a phenomenon known as conjugation. Conjugation is said to be taking place if two double bonds are separated by just one single bond. For example:
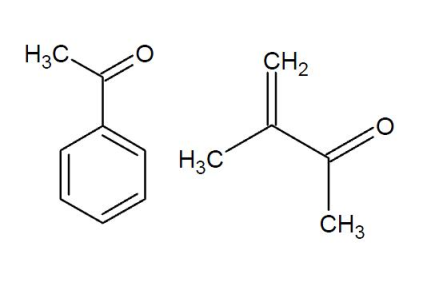
Conjugation lowers the frequency of the normaal stretch by ~30 cm$^{-1}$.
If the carbonyl forms part of a ring, then the smaller the size of the ring the higher the stretching frequency.This is due to the fact that on vibration, the carbon of the carbonyl group moves along with the oxygen but feels some resistance due to the C-C bonds it has with other carbons in the ring. The smaller the angle in the ring (and thus the smaller the ring itself), the more these C-C bonds are compressed during vibration. This compression requires more energy meaning a higher absorption frequency.
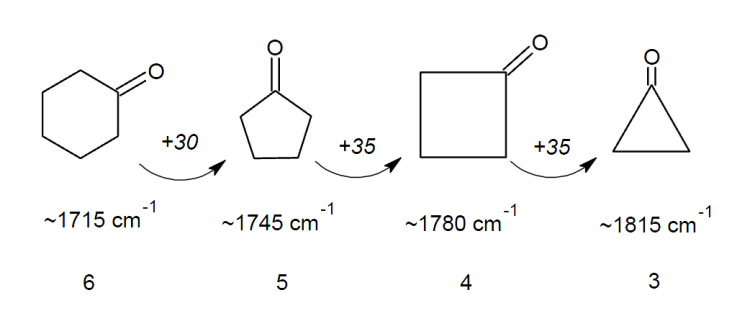
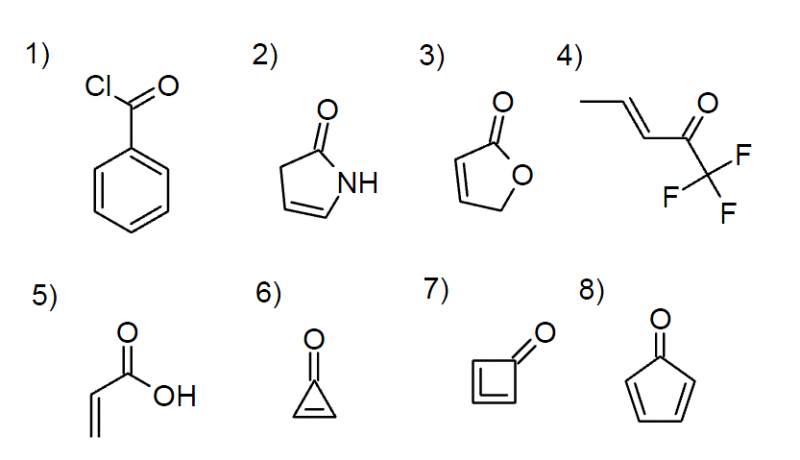
Using your newly gained knowledge on conjugation and ring strain, can you predict the carbonyl stretching frequencies of the following molecules?
Raman spectroscopy
$h\nu_{Stokes}$ = $h\nu_{L} - (E_{upper} - E_{lower})$
The anti-Stokes scattering is the energy change accompanying a fall in molecular energy level.
$h\nu_{anti-Stokes}$ = $h\nu_{L} + (E_{upper} - E_{lower})$
Measuring this energy shift enable us to measure the separation between molecular energy levels.
Vibrational energy level $\nu$ = 0 is the only state significantly populated, so the most intense scattering comes from the transition between $\nu$ = 0 and $\nu$ = 1.
Stokes photons with energy $h\nu_{Stokes}$ = $h\nu_{L} - \hbar\omega$, where $\hbar\omega$ is the energy separation between these two layers. The frequency of these photons is therefore:
$h\nu_{Stokes}$ = $h\nu_{L} - \hbar\omega$
$\nu_{Stokes}$ = $\nu_{L} - \frac{\omega}{2\pi}$
Raman spectroscopy is useful as there does not need to be a change in dipole moment during vibration, only the polarizability of the molecule has to change. The scattering is weak and so the detection equipment is quite complex.
