Mach Attack
Problem
A moving aeroplane is constantly hitting gas molecules, causing compression waves which move away from the aeroplane at the speed of sound.
If we simplify an aeroplane as a small, slowly moving particle that produces sound waves in all directions, then a 2D slice of the wavefronts in the $(x, y)$ plane would look like almost concentric circles, as follows: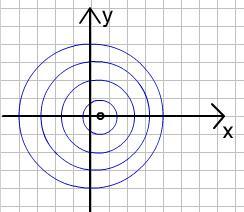
An aeroplane moving slowly, relative to the speed of sound
The speed of aeroplanes is measured in units of Mach $-$ Mach $1$ is the speed of sound, Mach $0.5$ is half the speed of sound, Mach $2$ is twice the speed of sound, and so on.
In the context of sound waves, why is Mach $1$ important?
Can you accurately draw the location of various wave fronts around the plane at Mach $0.5$? What about Mach $1$? What about Mach $2$?
What would the situation be for a typical commercial airplane?
Tip: A pair of compasses would help you to draw clearer circles.
With aircraft travelling above the speed of sound, the full 3D boundary of all of the wavefronts forms a simple solid shape. Can you find a way to describe this shape algebraically in terms of $v$ (the speed of the aeroplane) and $c$ (the speed of sound)? (Note that this shape is often visible around fast moving aircraft)
What goes wrong with the description of your shape for aircraft speeds slower than the speed of sound?
Aside: You can still make sense of this shape using complex numbers, although it does not 'exist' as such. You might like to investigate this idea to test out your skill with complex numbers. For example, how does the result relate to the physical situation? See the solution for more details.
Extension: You might like to think about the patterns of wavefronts for aircraft moving along curved trajectories.
Getting Started
Student Solutions
Draw a line of equally-spaced dots, representing the locations of the aeroplane at some time interval. You can work back from the last dot (the current location of the 'plane), and draw circles out from each dot representing where the wavefront would be, from when the 'plane was at that point. So for the case when $v = c/2$, draw a circle of radius 2 from the 2nd-last dot, 3 from the 3rd-last dot, and so on.
Above the speed of sound, a mach cone arises around the aircraft. This can often be seen. If you draw out the diagram as above for the case when the speed of the 'plane is greater than the speed of sound, you can see from trig that the semi-apex angle of the cone is equal to $\sin^{-1}{(c/v)}$.
A solution to the $\sin{\theta} = 2$ problem is here.
Teachers' Resources
This problem is aimed at interested and enthusiastic students: although we don't recommend it for mainstream classroom use it provides enrichment and will develop mathematical thinking and knowledge.
Like all NRICH problems it has been carefully designed to be full of mathematical interest and as such might be used in a variety of ways: you might suggest that keen students consider the problem in their own time, use it for a maths club at school or use it in class as a vehicle to foster discussion and mathematical thinking. See our Teachers Guide to Getting Started with rich tasks for more suggestions and ideas.
This problem will be of particular interest to students considering a university course containing an element of mathematical physics.
