Classical Means
Use the diagram to investigate the classical Pythagorean means.
Problem
For any two numbers $a$ and $b$ three classical Pythagorean means are defined, the arithmetic mean $A$, the geometric mean $G$ and the harmonic mean $H$ such that:
$$\eqalign{
A &= \frac{1}{2}(a+b) \cr
G &= \sqrt {ab}\cr
H &= \frac{2}{\frac{1}{a}+\frac{1}{b}}.}$$
(i) Prove that $H=\frac{G^2}{A}$.
Image
|
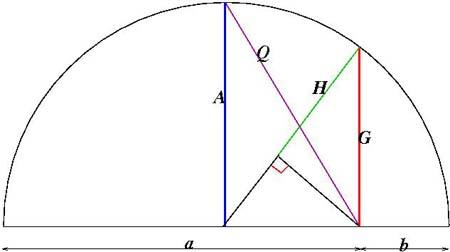
(ii) In this diagram the semicircle has diameter $a+b$. Prove
that the lengths $A$, $G$ and $H$ (shown in blue, red and green)
are equal to the three means and deduce from the diagram the
inequality
$$A> G> H.$$
|
(iii) Prove from the diagram that the length $Q$ is equal to the quadratic mean (or root mean square) such that $$Q=\sqrt{\frac {a^2+b^2}{2}}.$$
Getting Started
Don't overcomplicate things: Some of the parts of the problem are very simple!
For the trickier parts you will only need pythagoras and basic trigonometry.
Don't forget to think about the result!
Teachers' Resources
|
Why do this
problem?
Image
|
Doing this problem you need to visualise the relationship between the formulae for the arithmetic, geometric and harmonic means in terms of the radius of a circle and the geometry of similar triangles and Pythagoras Theorem. This process involves a beautiful blend of algebra and geometry. It provides a good exercise for learners in mathematical reasoning and proof. The mathematical concepts are simple and the interplay of ideas to give the necessary proofs is good experience for learners. |
Possible approach
Ask the learners to work out the radius of the semicircle in
terms of $a$ and $b$. Then ask them to identify all the triangles
and to discuss with a partner, and write down, everything they
observe about the triangles. They may then be able to do the
problem for themselves. If not the following questions should
provide some assistance.
Key questions
Can you find the radius of the semicircle?
Can you see a right-angled triangle with $G$ as the length of
one side and use this to find $G$ in terms of $a$ and $b$?
Can you use similar triangles to find a relationship between
$A$, $G$ and $H$?
Can you use similar triangles to find a formula for $H$ in
terms of $a$ and $b$?
Can you you use the geometry of triangles to compare the
lengths of $A$, $G$ and $H$?
Can you see a right-angled triangle with $Q$ as the length of
one side and use this to find $Q$ in terms of $a$ and $b$?
Possible
extension
Try the problem
Pythagorean Golden Means and read the article
About Pythagorean Golden Means
Possible support
Try the problem
Harmonic Triangle.
