Ideal axes
Problem
At constant temperature $T$, the gas law $PV=nRT$ is effectively an equation with two variables. Plotting different combinations of the variables $P$ and $V$ as the axes yields the three charts below. Can you deduce the likely variables and units for the axes in each case and the value for $nRT$? What is the likely physical interpretation of this value?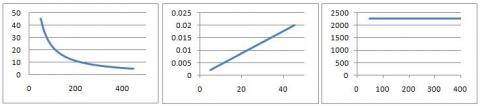
Explore the different possibilities for the shapes of graphs for the following equations by choosing different variables for the axes (you choose values for the constants)
Kinetic theory equations: Plot $PV = \frac{1}{3}mN\bar{c^2}$ for fixed $V$ and variable $P$, $\bar{c^2}$
van der Waals equations: Plot $(P+aV^{-2}_m)(V_m-b)=RT$ for fixed $T$ and variable $P$, $V_m$.
Can each be plotted in a form qualitatively similar to the three charts above? Can they be plotted to yield other forms distinct from the above?
You might wish to use a spreadsheet to allow you to make the various plots quickly, and you may wish to explore other formulas common to science.
Getting Started
Student Solutions
Using the graphs provided, you should have gained an appreciation for the different subtle variations in the pressure- volume relationship. In the context of the question, both $n$ and $T$ can be considered constants within the $PV = nRT$ equation. It may help to express the relationship as $P = \frac{nRT}{V}$.
The first of the given graphs displays an inverse relationship between the two variables. Considering the form $P = \frac{nRT}{V}$, this can be seen to be a plot of pressure compared to volume. The y axis given ranges from 0 to 50 units. This is likely to be the volume as pressure is usually given in units of pascals (1 Nm$^{-2}$). So we can say that the form of the graphical plot is something like $V = \frac{nRT}{P}$ where P is probably given in kPa as the value of atmospheric 1 bar pressure is 10^5 pascals. The volume could be is units of dm$^3$. This is working on an assumption that if we use quantities of 1 mole and 25$^o$C (298 K) we can calculate that an appropriate volume at a pressure of 200 kPa would be:
V = $\frac{1 \times 8.31 \times 298}{200 000}$ = 0.012382 m$^3$
Graphically, a value of around 10 units is seen and we can see that by scaling up by 1000, the value we have calculated is in the same approximate range as that on the graph. So units of dm$^3$ are appropriate.The value of nRT in this case is $0.01 \times 200,000$ = 2000 J = 2 kJ.
The second graph is a linear relationship of proportional increase. If we consider a modification of the above reciprocal plot, a plot of P vs 1/V or V vs 1/P are possible valid forms. If we consider a comparison between the first and second graph, the values on the x axis on the second graph correspond readily to the values on the y axis for the second graph. We can see that if we read off the first graph for a volume of 10 dm$^3$, the equivalent value of 1/P is $\frac{1}{200} = 0.005$ which is the same as the equivalent value on the second graph. This again maps for other possibilities. Units of the y axis in this case are by inference kPa$^{-1}$. The value of nRT putting in place these assumptions is again, 2kJ.
The third graph represents a situation where changing the value of the variable on the x axis does not change the value on the y axis. We already know that the value of nRT is fixed due to the fact that we are dealing with a situation where we have a constant number of moles and a constant temperature. As the axes must be in terms of the variables P and V, the y axis must be PV. The x axis can be either pressure or volume in sensible units. We can see again there is a similarity with the x axis of the first graph meaning the x axis is likely to be the variable P plotted in kPa for the reasons stated before. The value of nRT can be simply read off the graph to be 2250 J = 2.25 kJ.
The value of nRT is proportional to the internal energy of the ideal gas with modest changes in volume and has units of energy. It is clear that changes in pressure are compensated for by changes in volume to ensure that the nRT value of the ideal gas is kept constant.
Note that the values of units and assignment of axes is merely one of many possible solutions. As long as there is a step by step logical process behind your answer then other assignments of axes and possible units may be equally valid.
The next part of the question is more open to investigation by a variety of means including the use of spreadsheets. An outline of some form of solution is given below.
Kinetic theory equation, PV = $\frac{1}{3}mN\bar{c^2}$
This equation can be rewritten as P = $\frac{mN}{3V}\bar{c^2}$ and where m is the momentum that a certain particle possesses, N is the number of particles and $\bar{c^2}$ is the mean square velocity of a molecule (resolved in all component directions).
The inverse relationship may be generated by plotting P against $\frac{1}{\bar{c}}$ but clearly the gradient of the limbs of the graph and the transition is different from a $\frac{1}{\bar{c^2}}$ which can be seen easily using a spreadsheet or considering the change in P with variations in $\bar{c}$. Again if we plot P against $\bar{c^2}$ we obtain a linear relationship similar to graph 2. If we plot $\frac{P}{\bar{c}}$ against $\bar{c}$ a linear relationship is also observed. The constant term is clearly $\frac{P}{\bar{c^2}}$ and a graph qualitatively the same as the third may be obtained by plotting this against P or ${\bar{c^2}}$.
Plotting P against $\bar{c}$ gives a squared relationship. Plotting P against $\frac{1}{\bar{c}}$, as we have already considered, gives an interesting variation to the first graph.
You might like to consider the appropriate units to use for your axes given your choice of constants.
Van der Waals equations, $(P + aV_m^{-2})(V_m - b) = RT$
In this case all terms are constant apart from the terms $P$ and $V_m$, corresponding to pressure and volume. Expansion and rearrangement of this equation gives:
$\frac{-ab}{V_m^2} + \frac{a}{V_m} + V_mP - Pb = RT$
$V_mP - Pb = \frac{ab}{V_m^2} + \frac{-a}{V_m} + RT$
$P = \frac{ab - aV_m + RTV_m^2}{V_m^3 - bVm^2}$
The quadratic numerator in terms of $V_m$ is the numerator and a cubic equation in $V_m$ the denominator in the LHS fraction. Thus broadly speaking a plot of P against $V_m$ yields a relationship similar to that in graph 1, as this again a type of reciprocal relationship. Plots of P against $V_m^2$ and P against $V_m^3$ would also yield a plot that looks similar to the first. There are many other plots that can yield this approximate relationship including that of \frac{1}{V} against \frac{1}{P}.
How many can you find? Using a spreadsheet or analytical methods, can you describe what the differences are between each of these reciprocal plots?
Consider the case when a and b are 0. If we then plot P against $\frac{1}{V_m}$ a straight line relationship can be produced. This is clear after viewing the algebraic form above as you generate a $PV_m = RT$ type relationship.Plotting $(P + V_m^{-2})(V_m)$ against P yields a relationship that is close to a straight line. If we also consider that our constant term is RT, then we can effectively plot a relationship (P + V_m^2)(V_m - 1), where both a=1 and b=1 (for simplicity), against either V_m or P to yield a plot similar to the third graph.
An interesting plot is that of P against $\frac{1}{V_m^2}$ and $\frac{1}{V_m^3}$which gives a graph with a diminishing gradient over time. Plotting these two relationships on the same graph and observing the difference between these trends would be an interesting comparative exercise. A plot of P against $\frac{1}{V_m}$ also gives a trend with an increasing gradient over time.The form of this is again dependent on the values of your constants.
Experiment what happens on variation of these values, for example when they are very large and when they become increasingly close to zero.
There are many other examples of plots and the aim of this task is to find as many interesting alternatives as possible.
