Hold still please
Problem
Imagine holding a set of point charges at fixed positions in space - you can choose how many, the positions and the sizes of the different charges.
Experiment with different configurations of charges to determine whether you could arrange the charges so that when released simultaneously none of them starts to move.
Could you arrange the charges so that when released simultaneously only $1$ or $2$ of them start to move?
You might use your intuition to explore various possible configurations, but you will need to use Coulomb's law to show that the vector force on a particular particle is zero (see the Notes below) to prove your results.
Imagine that you are allowed to hold fixed one or more of the charges. What are the possibilities now?
Do your configurations seem stable to slight perturbations, in that they won't fly apart when subjected to a slight nudge? How might you create a stable configuration to confine a charged particle?
NOTES AND BACKGROUND
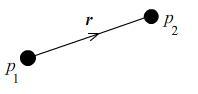
| Coulomb's law states that the electrostatic force ${\bf F_{12}}$ a charged particle $p_1$ of charge $q_1$ feels due to the presence of another charged particle $p_2$ of charge $q_2$ is $${\bf F_{12}} = -\frac{kq_1q_2}{r^2}{\bf \hat{r}}\,,$$ where ${\bf r}$ is the vector displacement of $p_2$ from $p_1$and $k$ is a positive constant, the value of which depends on the electrostatic permittivity of the medium in which the charges reside | Image
|
Getting Started
Don't forget that the total vector force on a particle equals the vector sum of the forces from all other particles.
For an unconstrained particle not to move, the total force on the particle must equal the zero vector.
Student Solutions
Clearly, a configuration of just 2 charged particles cannot remain stationary.
I then considered a configuration of 3 charges particles.
I considered whether an equilateral triangle of like charges, with an unlike charge in the centre, could be finely balanced in a plane. Of course any nudge outside of the plane would break the equilibrium. This has the potential to be stable: consider particle $A$ in the diagram; the horizontal force from particles $C$ and $B$ will cancel out leaving a net force in the positive vertical direction. By choosing the magnitude of the central force, we can cancel out this force.
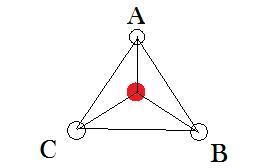
To see how this would work in detail, I resolved the forces at one vertex of the triangle, in the direction the vertex is pointing, and letting the side length of the equilateral triangle be $d$, and the vertex charge be $q_v$, and the central charge be $q_c$, I could say that
$$
F_A = 0 = 2\frac{kq_vq_v}{d^2}\cos30 - \frac{kq_cq_v}{\left(\frac{d}{\sqrt{3}}\right)^2}
$$
$\therefore q_v = \sqrt{3}q_c$ would satisfy this arrangement.
Seeing this, I wondered if it might be possible to find a general result for a regular polygon with a central unlike charge (perhaps $q_v = \sqrt{\mbox{polygon order}}q_c$?)
But resolving the same way on a square, we find that
$$
F_A = 0 = 2\frac{kq_vq_v}{d^2}\cos45 + \frac{kq_vq_v}{\left(\sqrt{2}d\right)^2} - \frac{kq_cq_v}{\left(\frac{d}{\sqrt{2}}\right)^2} \rightarrow q_c = \frac{2\sqrt{2} + 1}{4}q_v \rightarrow
$$
no obvious correlation between the order of the polygon and the required relationship between the charge for equilibrium, in fact the direction of the trend is the opposite. $q_v \approx 1.73q_c$ for a triangle and $q_v \approx 1.045q_c$ for a square.
I am reasonably convinced by this that it would be possible to find a stable choice of charges for any regular polygon with an unlike charge in the centre.
I am also sure it would work for a regular polyhedron.
It is not possible to have an arrangement such that only one charge moves due to Newton 3. It is possible that only 2 move, for example three like charges equally spaced
If one were fixed, of course it would be possible that just one could move.
As mentioned, the planar configurations above are not stable. But what about a 3-D configuration, such as a tetrahedron with an unlike charge in the centre?
I wondered if a tetrahedral arrangement would be stable, and decide to find the appropriate charges, and then mathematically move the central charge by an amount $\delta$, to see if the result was enlightening.
Thinking about and drawing out a regular tetrahedron of edge length $l$, I can see that it can be made from 3 triangular pyramids. I calculated the dimensions by looking at a cross-section of the tetrahedron and seeing a right-angled triangle of hypotenuse $l$, base $\frac{l}{\sqrt{3}}$, and of side (pyramid height + pyramid side edge length) (calling them $h + s$). From trig, we know this sum is $\sqrt{\frac{2}{3}}l$, so we have that equation and we also have the fact that $s^2 = h^2 + (\frac{l}{\sqrt{3}})^2$ from the pyramid itself. Combining these we can find that $s = \sqrt{\frac{3}{8}}l$ and $h = \frac{\sqrt{6}}{12}l$. The central vertices of these pyramids meet in the centre of the tetrahedron. This helped me to formulate the Coulomb's law equation, again resolving forces at a vertex of the shape, and again in the direction the vertex is pointing, $\frac{3q_vq_v}{l^2}\cos(\theta) = \frac{q_cq_v}{\left(\sqrt{\frac{3}{8}}l\right)^2}$, where $\cos(\theta) = h/s = 1/3 \therefore q_v = \frac{8}{3}q_c\;.$
Having done this, I was glad it was an interesting exercise in proving the earlier part of the question in 3D rather than simple planar arrangements, because I realised it probably wasn't necessary for the last part of the question. Because it looks quite simply that if you move the central charge some amount $\delta$ towards a vertex, that vertex will have a net attractive force, and the other vertices will have a net repulsive force, and so the arrangement will tend to fly apart. Although I did not reach a conclusive mathematical proof of this.
One possibility for a stable configuration might be to have unlike charges orbiting. We know from our own solar system that mathematically similar arrangments are not broken up by slight nudges.
