Succession in Randomia
By tossing a coin one of three princes is chosen to be the next King of Randomia. Does each prince have an equal chance of taking the throne?
Problem
King At the first of Randomia has a problem. He is the proud father of three sons: Bingo, Toto and Lotto. Only one of the sons can succeed him as king but they are all suitable to rule the kingdom. At his wit's end he decides to use the following method to decide who his successor will be:
At a succession ceremony, the king will toss a coin repeatedly until two consecutive heads or two consecutive tails come up.
Bingo will become king if it is two successive heads (...HH) and this occurs in an even number of tosses.
Toto will become king if it is two tails (...TT) and this occurs in an even number of tosses.
Lotto will become king if it is either two heads (...HH) or two tails (...TT) and this occurs in an odd number of tosses.
The subjects are in an uproar because they think this method of selection is not fair.
Investigate the situation and decide whether or not the sons have an equal chance of becoming the next king. Talk to other people about it, people tend to disagree about this one so you need to have good reasons for what you think. How could you test out your theories?
(Thanks to Bertus van Etten and the Institute for Mathematics and Science Teaching of the University of Stellenbosch for permission to publish this problem.)
Getting Started
You can try an experiment to test this method but you will need to repeat the trials many times to reach any convincing conclusion. This would be a good class project.
A tree diagram will help you to analyse what happens. Try calculating the probabilities for 2, 3, 4, 5 and 6 ... tosses and see if you can identify a pattern emerging.
You could try to calculate the final probabilities. Theoretically the coin tossing can go on for ever so you will need to know a bit about summing an infinite series.
Student Solutions
Many good solutions to this problem were sent in. The best ones came from Alex from Stoke on Trent Sixth Form College, Katie from Firhill High School Edinburgh, Andrew from St Aidan's RC School, Sunderland, David from Queen Elizabeth High, and Tom from Devonport Boys School. Andrew and Katie's reasoning relate to a tree diagram. Tom's solution appears below.
At a glance the statement seems illogical. Many people think at first that the process is unfair. Often people do not understand that by doing a coin tossing experiment to see how many trials result in each brother being chosen they only get an experimental probability that may be very different to the actual probability. The tree diagram (which may be extended indefinitely) shows the actual probabilitites. It is easy to demonstrate the fairness of this process as a way of choosing between three options.
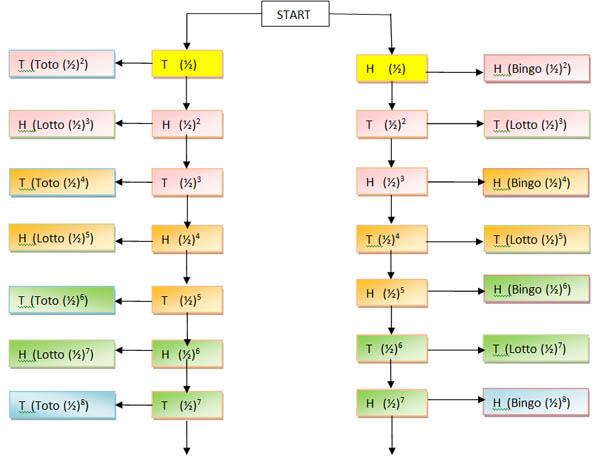
In the tree diagram, the boxes on the right and left show a final decision. The coin tossing can go on indefinitely if no two successive heads or tails occur as shown by the vertical lines in the diagram.
Each set of 8 boxes with the same colour denotes a round of two tosses but we do not start Round 1 from the first toss (yellow) as no decision can be made until the second toss.
Note that the first throw in each round is an 'even' throw, the second an 'odd' throw.
Consider Round 1 (pink), the second and third tosses. Note that a third toss may not be necessary if the new king is chosen at the second toss. Each brother has a total probability of $0.25$ of being chosen and the probability of there being no result and going on to the next round is $0.125+0.125 = 0.25$.
So in any round: when the previous round ended on a head the next few throws could be:
(H)H,H --> Bingo (the final H is irrelevant, bingo has already won)
(H)H,T --> Bingo
(H)T,H --> No result
(H)T,T --> Lotto
When the previous round ended on a tail the possibilities are:
(T)H,H --> Lotto
(T)H,T --> No result
(T)T,H --> Toto
(T)T,T --> Toto
Consider Round 2 (orange), the fourth and fifth tosses. Note that a fifth toss may not be necessary if the new king is chosen at the fourth toss. Now from rounds 1 and 2 together, each brother has a total probability of $(0.25+(0.25)^2=5/16 $ of being chosen and the probability of there being no result and going on to the next round is $2(1/32)=1/16 =1 - 15/16$.
Tom's spreadsheet shows the calculations correct to 8 decimal places for 31 tosses, (15 rounds). We can see that, earlier on, the chances of each brother being chosen are nearly the same and we can also see that the probability of alternate heads and tails and no result being decided gets closer and closer to zero and the probabilities for each brother being chosen get closer to one third.
To find the total probability for Bingo being chosen we need to sum the following infinite geometric series (and the same series applies to the probability of Toto being chosen).
Probability of Bingo being chosen =$\frac{1}{4}+(\frac{1}{4})^2+(\frac{1}{4})^3+(\frac{1}{4})^4 \cdots = \frac{\frac{1}{4}}{1 - \frac{1}{4}}= \frac{1}{3}$.
As the probability of the process going on for ever with no decision is $\lim_{n\to\infty}(\frac{1}{4})^n = 0$ it follows that each brother has a probability of one third of being chosen.
Teachers' Resources
Why do this problem?
Here you have to interpret the information given in the problem, decide whether or not the method of choosing the new king seems fair, and decide what methods you might use to check on whether it is fair or not. It is a novel context and yet easy to understand what the problem is. No resources are needed to run trials except some coins.
Then you need to decide what the possibilities are, what the probability space is and what would constitute a 'trial' to test the relative frequencies of the different possible outcomes.
The problem can be tackled at different levels. It can be treated as an investigation into the experimental probability. Alternatively, learners can draw a tree diagram and calculate the probabilities using a computer program or spreadsheet. Those who have met geometric series should be able to calculate the theoretical probabilities.
Possible approach
Why not start with a class referendum on whether the King's method is fair? Let the learners discuss it in pairs and then as a class and then take a vote. Many learners will think it is not fair because they think Lotto has a better chance as he wins the throne if he gets either two heads or two tails whereas his brothers only win with one or the other.
You could make each pair of learners run 10 or more trials, one tossing the coin until two successive heads or two successive tails come up, and the other recording the results and which son would be king for each trial. Then you could put all the class results together and calculate the relative frequencies. Is the relative frequency for selecting each son approximately one third?
Commonly learners find this problem hard because the probability space has infinitely many events. The class can discuss what the events are and how they fall into four sets of events.
The next task could be to draw a tree diagram and to use this to help to calculate the probabilities after 2, 3, 4, 5, 6, 7, 8 ... events so as to identify the pattern emerging.
A spreadsheet helps with these calculations. Considering only up to 8 tosses the probabilities are (to 4 decimal places): Bingo 0.3320, Toto 0.3320, Lotto 0.3281, still undecided 0.0078. Notice that the probabilities get closer and closer to one third and after 8 tosses you can go on to find out how that 0.0078 is distributed between the three brothers.
For learners who can sum an infinite geometric series, the calculation of the theoretical probability is easy as it only involves powers of one half.
Key questions
What are the possible outcomes?
Could the coin tossing go on for ever without a decision being reached? How likely is that? Why?
What are the probabilities for each son being chosen after two coin tosses?
If no decision is reached after two tosses what are each son's chances with 3 tosses?
If no decision is reached after three tosses what are each son's chances after 4 tosses?
Can you draw a tree diagram?
Can you use a spreadsheet to help with the calculations?
Can you write down the series that you would need to sum to find the probability of Bingo being chosen?
What are the total theoretical probabilities of each of the 4 possible outcomes: Bingo being chosen, Toto being chosen, Lotto being chosen, the coin tossing going on for ever?
Possible extension
For many learners this problem will only involve testing the relative frequencies. For others the extension will be calculating the theoretical probabilities. The problem Rain or Shine requires similar reasoning and is a good one to follow Succession in Randomia.
Possible support
For those who are convinced that Lotto has a better chance and that the relative frequencies should not turn out all to be approximately one third for a large number of trials, suggest that they consider the answers to the key question: "Bingo and Toto are always ahead when there have been an even number of tosses and Lotto's chances only 'catch up' when the next toss is made to give an odd number of tosses, how then can Lotto ever be ahead?"
