Bicentric Quadrilaterals
Investigate the properties of quadrilaterals which can be drawn
with a circle just touching each side and another circle just
touching each vertex.
Problem
First, try the problem Circles in Quadrilaterals to familiarise yourself with the properties of tangential quadrilaterals.
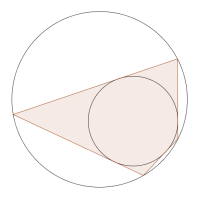
A bicentric quadrilateral is both tangential and cyclic. In other words, it is possible to draw a circle inside it which touches all four sides, and also to draw another circle around it which passes through all four vertices. (The two circles do not necessarily have the same centre!)
Here is a picture of a bicentric quadrilateral.
Image
Think about special quadrilaterals,
such as squares, trapezia, and parallelograms.
- Which types of quadrilateral are always bicentric?
- Which types of quadrilateral are never bicentric?
- For the quadrilaterals which are sometimes bicentric, can you explain the conditions necessary for them to be bicentric?
There is a formula for finding the area $A$ of a bicentric
quadrilateral:
$$ A = \sqrt{abcd} $$
where $a,b,c$ and $d$ are the lengths of the four sides.
Verify that this formula gives the correct area for the
examples of bicentric quadrilaterals you have found.
Getting Started
Start by deciding which quadrilaterals can be tangential. What
conditions also need to be satisfied to ensure the quadrilateral is
also cyclic?
Student Solutions
We
received a great solution from Zhi of St. Marylebone CE School. She
begins with a diagram:
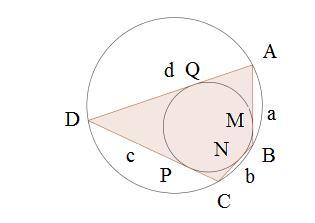
In the diagram presented, the vertices of the quadrilateral are labeled A, B, C and D, and tangent points M, N, P and Q respectively. The sides are labelled a, b, c and d.
From the properties of the circles we know that the tangents AM and AQ, BM and BN, CN and CP, DP and DQ are equal respectively. Therefore, if the quadrilateral is to be tangential, AQ+DQ+BN+CN would have to be equal to AM+DP+BM+CP, which then becomes:
$$AD+BC=AB+CD$$ Therefore, we know that a tangential quadrilateral has to satisfy AD+BC=AB+CD.
Using the properties of isosceles triangles and angle bisectors, we can deduce that the reverse is also true, meaning that all quadrilaterals satisfying $AD+BC=AB+CD$ are tangential. Is the reverse obvious? The question only asks for a necessary condition so in fact we do no need to show the reverse but this could be a nice extension.
The properties of cyclic quadrilaterals imply that for any cyclic quadrilateral ABCD, $\angle A+\angle C = \angle B +\angle D = 180^{\circ}$.The reverse is also true. Can you show this condition is necessary? See the problem Circles in Quadrilaterals.
Image

In the diagram presented, the vertices of the quadrilateral are labeled A, B, C and D, and tangent points M, N, P and Q respectively. The sides are labelled a, b, c and d.
From the properties of the circles we know that the tangents AM and AQ, BM and BN, CN and CP, DP and DQ are equal respectively. Therefore, if the quadrilateral is to be tangential, AQ+DQ+BN+CN would have to be equal to AM+DP+BM+CP, which then becomes:
$$AD+BC=AB+CD$$ Therefore, we know that a tangential quadrilateral has to satisfy AD+BC=AB+CD.
Using the properties of isosceles triangles and angle bisectors, we can deduce that the reverse is also true, meaning that all quadrilaterals satisfying $AD+BC=AB+CD$ are tangential. Is the reverse obvious? The question only asks for a necessary condition so in fact we do no need to show the reverse but this could be a nice extension.
The properties of cyclic quadrilaterals imply that for any cyclic quadrilateral ABCD, $\angle A+\angle C = \angle B +\angle D = 180^{\circ}$.The reverse is also true. Can you show this condition is necessary? See the problem Circles in Quadrilaterals.
Therefore, a bicentric
quadrilateral ABCD has to meet two conditions
- $AD+BD=AB+CD$ and
- $\angle A + \angle C = \angle B +\angle D = 180 ^{\circ}$
With that , we can now
deduce:
- Squares are always bicentric
- Rectangles and rhombi, provided that they aren't squares, cannot be bicentric as rectangles do not satisfy condition 1, and rhombi do not satisfy condtion 2.
- Irregular parallelograms do not meet either condition and cannot be bicentric
- Trapezia might or might not be bicentric, depending on their side lengths and angles.
Zhi then went on to prove the formula for the
area of a bicentric quadrilateral. We shall omit the proof here
since the question only asks you to verify that the formula works
on the examples you found. If you are interested see the proof of
brahmagupta's formula and try to adapt it to this
problem.
Teachers' Resources
Why do this problem
This problem provides an opportunity to consider properties of quadrilaterals and circle theorems while investigating the unfamiliar and intriguing idea of bicentric quadrilaterals.Possible approach
First, try the problem Circles
in Quadrilaterals. For learners who are unfamiliar with the
properties of cyclic quadrilaterals, the problems Triangles
in Circles and Pegboard
Quads can be used to investigate.
Explain that a bicentric quadrilateral is both cyclic and
tangential, so a circle can be drawn inside it just touching each
side, and another circle (not necessarily with the same centre) can
be drawn around it just touching each vertex. Ask learners to
sketch examples of bicentric quadrilaterals, and encourage them to
share ideas in pairs about how to identify which quadrilaterals are
bicentric.
Bring the class together for discussion of their ideas. One
hint for finding bicentric quadrilaterals is to start with a
tangential one and make it also cyclic, or vice versa.
Experimenting with a dynamic geometry package such as Geogebra can give some insight
into the properties of these quadrilaterals.
Then give pairs or small groups time to construct some
examples of bicentric quadrilaterals and calculate their areas. The
areas can then be used to verify the area formula given for these
cases.
Key questions
What properties must a quadrilateral have to be
tangential?
What properties must a quadrilateral have to be cyclic?
Which quadrilaterals can be both tangential and cyclic at the
same time?
Possible extension
Show that the area formula given will hold for specific types of quadrilateral such as squares and kites, given the constraint that they are bicentric. Proving the formula generally is extremely challenging!Possible support
Try Triangles
in Circles as a basis for investigating circle theorems.
