Circles in Quadrilaterals
Explore when it is possible to construct a circle which just touches all four sides of a quadrilateral.
Problem
Circles in Quadrilaterals printable sheet
You may have come across the idea of a cyclic quadrilateral, where it is possible to draw a circle around the quadrilateral so that the circumference passes through all four vertices of the shape.
A tangential quadrilateral is one where it is possible to draw a circle inside it so that the circumference just touches all four sides of the shape.
Here are some examples of tangential quadrilaterals:
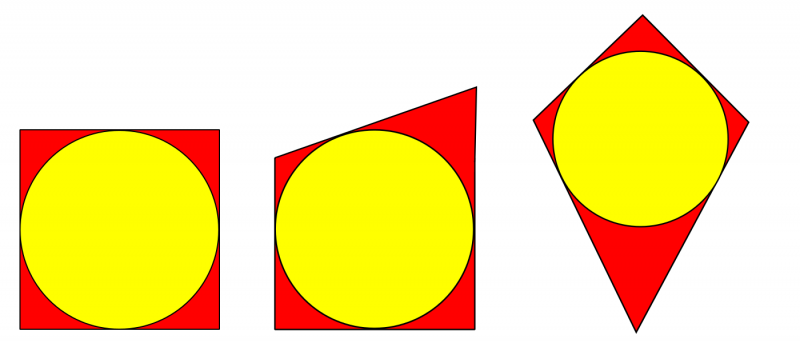
For each of the following types of quadrilaterals, decide whether it is always, sometimes or never possible to construct a circle inside which just touches all four sides:
- Square
- Rectangle
- Rhombus
- Parallelogram
- Kite
- Trapezium
Getting Started
Here I have drawn a semicircle which just touches a triangle.

Student Solutions
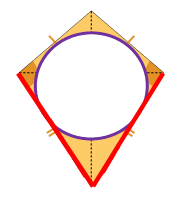
Preveina from Crest Girls' Academy sent us some pictures to support her reasoning about some of the shapes in this problem:
A circle can be always fitted in a square touching all 4 sides since the sides of a square are all equal. This makes the circle touch each side of the square evenly.
A circle can never be fitted in to a rectangle touching all 4 sides because a rectangle has 2 long sides and 2 short sides. When you're trying to draw a circle that touches all 4 sides in a rectangle it'll turn out to be an oval, since there are 2 long sides.



Teachers' Resources
Why do this problem?
This problem provides an opportunity for rich discussion of properties of quadrilaterals and circles, and leads to geometrical reasoning in searching for proofs and counter-examples.
Possible approach
This printable worksheet may be useful: Circles in Quadrilaterals.
Show the three examples of tangential quadrilaterals and allow the learners to identify what they have in common. Share the definition of a tangential quadrilateral as one where a circle can be constructed inside to just touch all four sides. This is called an inscribed circle.
Key questions
When is it possible to draw a circle inside a kite? a trapezium?
Possible support
Create lots of diagrams to build up ideas of what is and isn't possible. There is a diagram in Getting Started showing a semicircle constructed in a triangle; considering this may be helpful for those quadrilaterals which can be cut along a line of symmetry into two triangles.
Possible extension
If the side lengths of a tangential quadrilateral are $a$, $b$, $c$ and $d$, with $a$ opposite $c$ and $b$ opposite $d$, show that $a+c = b+d$.
