Lennard Jones potential
Investigate why the Lennard-Jones potential gives a good approximate explanation for the behaviour of atoms at close ranges
Problem
At a simple level, two interacting neutral atoms are subject to two opposing forces: firstly, they are weakly attracted by van der Waals forces; secondly they are repelled by Pauli repulsion. It is known that the van der Waals forces decay proportional to the sixth power of the separation and that the effects of the Pauli repulsion decay exponentially.
In 1924 it was suggested by Lennard and Jones that the potential energy of a system of two atoms separated by a distance $r$ could be approximated by
where $\epsilon$ and $\sigma$ are constants which are determined experimentally.
Think about this expression. What features might make it a sensible candidate for a model of reality?
A pair of atoms are brought together and the interaction energy measured. The results are plotted in the following chart:
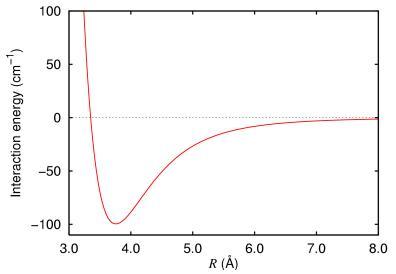
Experiment with the constants to determine how well the Lennard-Jones potential can be used to model this potential energy.
Suppose that another potential energy curve $W(r)$ was suggested as follows:
How does $W(r)$ differ from the Lennard Jones potential? Do you think that $W(r)$ could yield a good match with reality with a good choice of constants $\epsilon_w$ and $\sigma_w$?
John Lennard-Jones is considered to be the father of computational chemistry. This form of the potential has little theoretical justification, but sometimes matches reality to an acceptable standard. Its use greatly simplifies numerical calculations based on the inter-atomic potential.
Image taken from http://commons.wikimedia.org/wiki/File:Argon_dimer_potential.png
Getting Started
Think about the strength of attraction between molecules at a close distance and a far distance. Also, will they attract each other indefinitely, or will they repel at some small distance?
Student Solutions
The Lennard Jones potential has several features which might make it a suitable model for reality. This is best realised by looking at the plot of the function:
(a) As the separation of the two atoms increases, the attraction between them increases and tends to zero at infinite distance. This is sensible, since as two atoms approach each other from a large separation, their potential energy slowly drops as they are attracted together. Mathematically this is seen by the fact that both terms in the potential energy expression tend to zero as $r$ tends to infinity.
(b) There is a potential energy minima, which is the stable atomic separation. We know that the atoms ARE attracted to each other by van der Waals attractions, and so it makes sense that there will be some fixed distance apart that they will remain. Mathematically, this is as the turning point of the function, where the gradient is equal to zero.
(c) As the separation of the atoms decreases further, the potential rises sharply, which indicates that it is highly unfavourable for the atoms to be squashed together further. This is seen in reality, where two neutral atoms do not increasingly approach each other indefinitely! Mathematically, this is the $\left(\frac{\sigma}{r}\right)^{12}$ dominating the other term, which leads to a very positive potential as $ r$ decreases.
The $W(r)$ potential curve differs from the Lennard-Jones potential as it has a term to the power of $9$ as opposed to $12$. Consequently, the curve still tends to zero at infinity, still has a potential energy minima, and increases sharply with small $r$. Therefore it could well yield a good match with reality with appropriate values of the constants.
