Folding Fractions
What fractions can you divide the diagonal of a square into by simple folding?
Problem
You may wish to look at Folding squares before trying this problem.
|
Image
Image
|
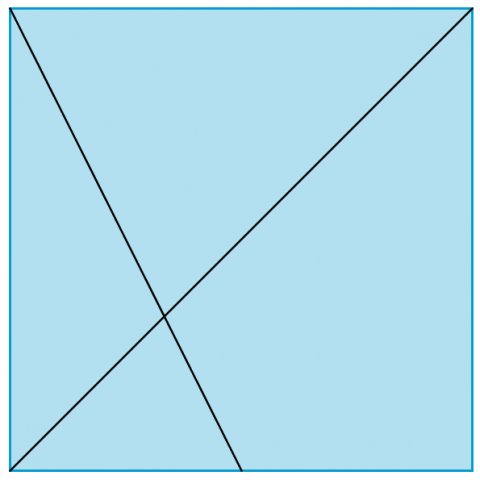
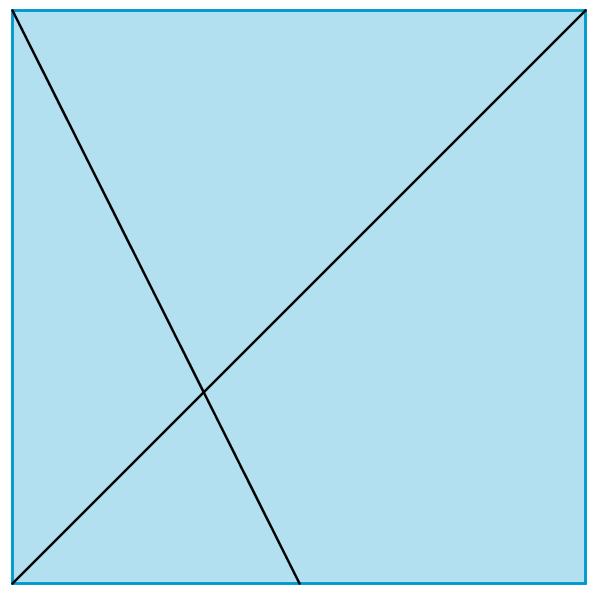
You can divide the long diagonal of a square into different fractions by folding.
This problem is about the fractions of the long diagonal of a square which you can construct in this way.
To start with, we shall only consider points on the side of the square which can easily be found by folding. That is, $\frac{1}{2}$s or $\frac{1}{4}$s or $\frac{1}{8}$s and so on.
|
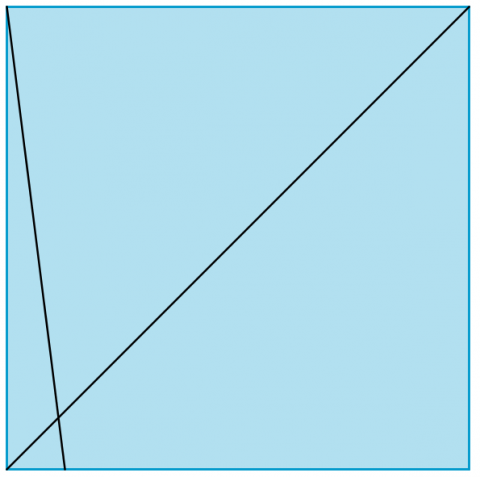
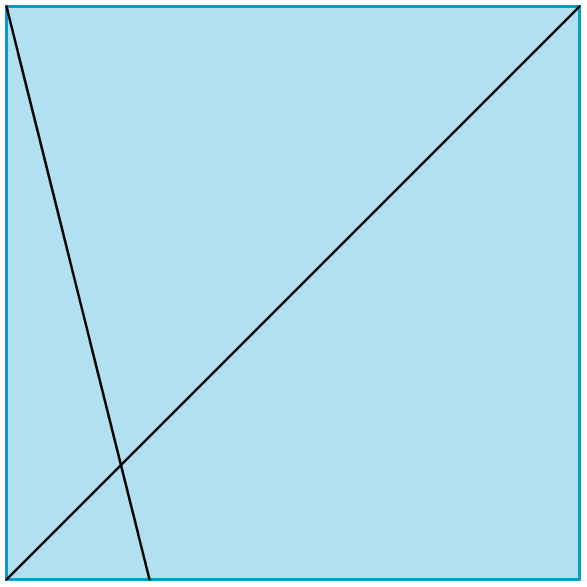
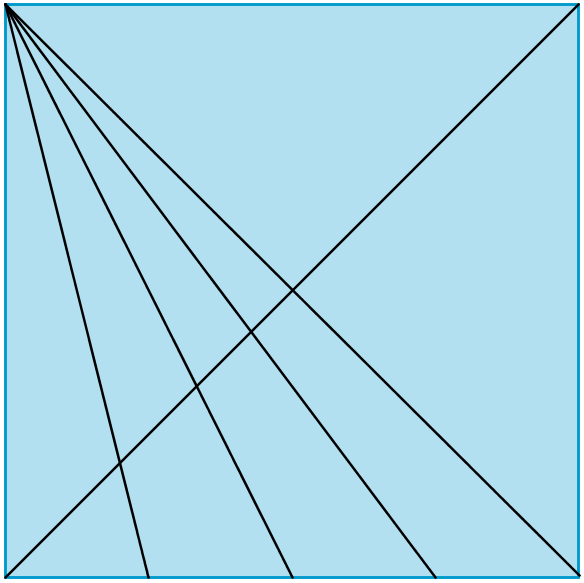
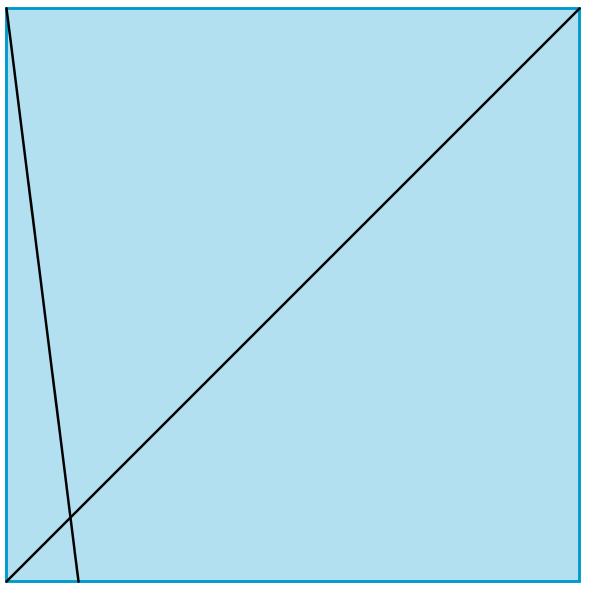
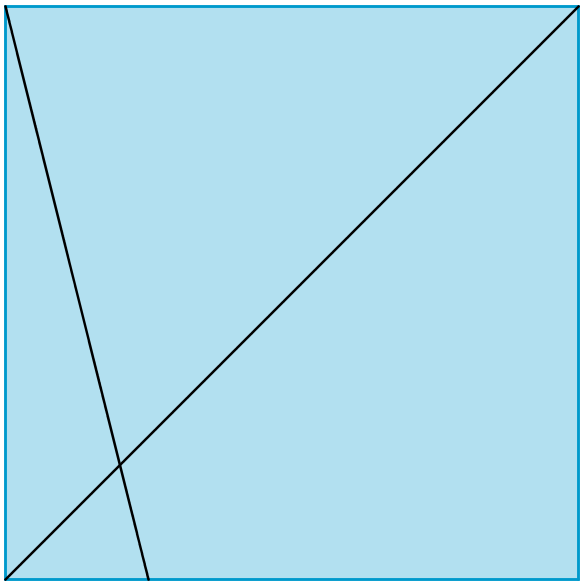
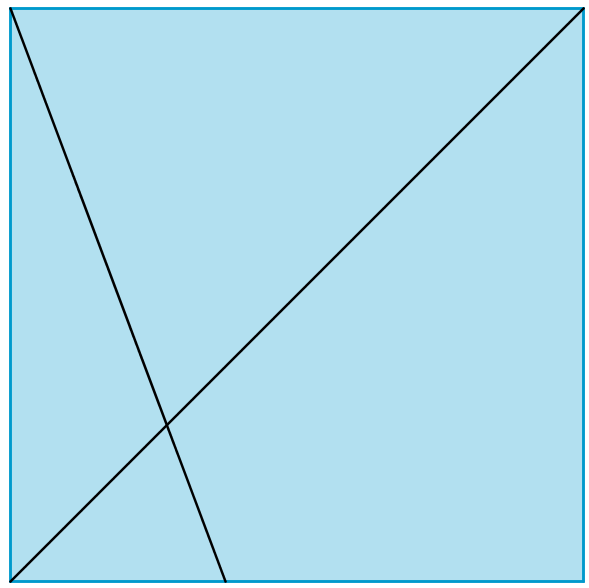
Investigate the fractions of the long diagonal of a square that can be created in the way described above. Here are some examples to think about:
Image
Image
Image

Image

Image
Image
Image
Image
Image

Image

Can you extend the findings and make generalisations?
Can you justify your generalisations?
What about starting with fractions of the side of the square that are not so easily found by folding?
Getting Started
Look for angles which are equal. Can you find any pairs of similar
triangles?
Student Solutions
Richard of Mearns Castle High School sent us in this solution:
Image
Notice that $AE = \frac{1}{n} AB = \frac{1}{n}x$
We can say that $\triangle AEF$ and $\triangle DCF$ are similar. This is because $\angle AFE$ is equal to $\angle DFC$ (vertically opposite). Also $\angle FAE = \angle FCD$ and $\angle AEF = \angle CDF$ (alternate angles).
Since the triangles are similar we can say that the ratios of corresponding sides are the same. Therefore:
$$\eqalign{
\frac {DC}{AE} &= \frac{FC}{AF}\cr
\frac{x}{\frac{x}{n}}&= \frac{FC}{AF}\cr
n &= \frac{FC}{AF}
}$$
Hence$$FC = AF \times n $$
So $DE$ cuts $AC$ at the ratio $1:n$.
Teachers' Resources
Why do this problem?
This problem investigates in more detail the relationships found in Folding Squares.
Relationships can be discovered by making accurate paper folds or diagrams, but there is also scope for some sophisticated geometrical reasoning, manipulation of fractions and finding and justifying general rules for the different fractions that can be made.Possible approach
Learners could start by marking off quarters along one side of a square, and making folds from the corner to these marks, as shown in the diagrams. Pose the question "What fraction of the diagonal do you think is formed by the line joining to a quarter of the way along the side? Half way? Three quarters?"
Learners can measure the lengths of the lines on their diagram to see if their conjectures appear to be right - they may be surprised by the results.
Once they have built up a picture of what is happening with quarters, they can investigate what happens when the side is divided into eighths. As it is not always easy to measure accurately enough and the fractions are not always obvious, learners might think about how to work more systematically and/or decide to use a more analytical approach. Moving them towards more formal and less
experimental methods could be encouraged through discussion and sharing of ideas.
Groups may wish to present their findings through posters.
Key questions
How can you organise your work so that you are able to identify any patterns that emerge?
How can you be sure of the fractions that appear to be emerging when you measure?
What mathematics have you met before that might be useful here?
What do you think would happen if we divided the side into fifths? Sixths?
Possible extension
If I divided the side of my square into $n$ equal portions, what fraction of the diagonal would I get by folding to $\frac{m}{n}$ of the way along the side?
What other quadrilaterials will this idea apply to and does the rule need modification in any particular cases?
