The pillar of Chios
Semicircles are drawn on the sides of a rectangle. Prove that the sum of the areas of the four crescents is equal to the area of the rectangle.
Problem
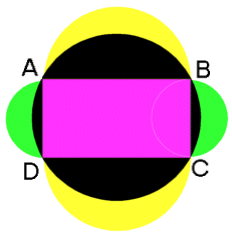
Semicircles are drawn on the sides of a rectangle ABCD as shown in the diagram. A circle passing through points ABCD carves out four crescent-shaped regions (coloured yellow and green in the diagram).
Prove that the sum of the areas of the four crescents is equal in area to the rectangle ABCD.
Student Solutions

The whole shape is made up of a rectangle, two semicircles on $AB$ and on $DC$ together making one circle, and the two semicircles on $AD$ and $BC$ making another circle.
Excellent solutions were sent in by a pupil from Dr Challoner's Grammar School, Amersham and Nisha Doshi ,Y9, The Mount School, York. Here is one of their solutions: Take: $AB=2x, AD=2y$.
By Pythagoras Theorem
so the sum of the areas of the four crescents is equal in area to the rectangle $ABCD$.
