Curvy Areas
Have a go at creating these images based on circles. What do you notice about the areas of the different sections?
Problem
Curvy Areas printable sheet
Curvy Areas downloadable slides
Take a look at the image below:

Can you see how the image was created?
Try to recreate it using a ruler and compasses.
Here are two images created in a similar way.


Can you work out the proportion of the 3-colour, 4-colour and 5-colour circles which is shaded red?
Can you make any generalisations?
Can you prove your ideas?
Extension
What about the proportion which is shaded orange? Yellow? ...
Can you make any generalisations?
Can you prove your ideas?
Getting Started
Suppose the radius of the smallest semicircle is $x$.
What are the radii of the other semicircles?
What areas can you work out, in terms of $x$ and $\pi$?
Student Solutions
There are so many ways of solving this problem we can't write them all here. Abdulla sent us a clear method for finding the areas in the first circle. The key observation is that the curvy areas are all cut out by circles and semicircles.
To work out the area of the sections of the circle I first drew a diameter through the circle and labelled the areas above the diameter $A$, $B$, and $C$.
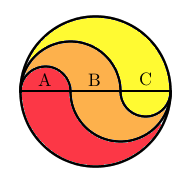
I used $x$ for the radius of the smallest semicircle $A$. It has an area of
$A=\frac{1}{2}\pi x^2$
The area $B$ is made from a semicircle radius $2x$, minus the area $A$.
Then $B=\frac{1}{2}\pi (2x)^2 - \frac{1}{2}\pi x^2 = \frac{3}{2}\pi x^2$.
Area $C$ is a semicircle radius $3x$ minus a semicircle radius $2x$. Then $C=\frac{9}{2}\pi x^2-2\pi x^2=\frac{5}{2}\pi x^2$.
We can use symmetry to calculate the coloured areas.
The red shaded area is $A+C=3\pi x^2$.
The orange shaded area is $2B=3\pi x^2$.
The yellow shaded area is $A+C=3\pi x^2$.
It turns out they are all the same, and are $\frac{1}{3}$ of the total shaded area.
Niharika sent in a good idea for generalising. She guessed that the shaded areas are always the same proportion of the total area and managed to prove it!
Instead of using $A$, $B$, $C$ for the areas as in the $n=3$ case, we can call them $A_1$, $A_2$, ..., $A_n$. Let the big circle have radius $r$. Then $A_1$ is a semicircle radius $r/n$, and each $A_k$ is a semicircle radius $kr/n$ minus a semicircle radius $(k-1)r/n$.

\begin{align}
A_k&=\frac{\pi}{2}\left(\frac{k^2r^2}{n^2}-\frac{(k-1)^2r^2}{n^2}\right)\\
&=\frac{\pi r^2}{2n^2}\left(2k-1\right)
\end{align}
And each shaded area coloured with the $k$th colour is made of a region area $A_k$ plus another area $A_{n+1-k}$. This is because the bottom half of the circle is the same as the top half, reflected and with the colours changed. Then the $k$th coloured shaded area is
\begin{align}
A_k+A_{n+1-k}&=\frac{\pi r^2}{2n^2}\left(2k-1\right)+\frac{\pi r^2}{2n^2}\left(2(n+1-k)-1\right)\\
&=\frac{\pi r^2}{2n^2}\left(2k-1 + 2n +2 -2k -1\right)\\
&=\frac{\pi r^2}{n}
\end{align}
Notice that this is $1/n$ of the total area $\pi r^2$ and it is the same for each of the $n$ colours (i.e. every $k$).
Fantastic work. Well done to everyone who found similar ways to generalise. Using algebra to deal with many different values at once, or unknown values is very important. In this question the calculations might be even easier if you work directly with fractions of area rather than with radii. Then there is no need to write down $\pi$.
Teachers' Resources
Why do this problem?
This problem offers the opportunity to practise calculating areas of semicircles and working in terms of $\pi$ and leads to a surprising result that invites students to generalise.
Possible approach
These printable resources may be useful: Curvy Areas,
Curvy Areas.
Begin by showing one of the three diagrams on these slides for a short while, then hide it.
"Think about the image you just saw. Can you make a sketch of it? Can you describe to your partner how it was drawn?"
Show the image again so that students can compare their first impression with the actual image. Recreating the image offers students a good opportunity for practising constructions with a pair of compasses.
"Now that we can see how the images were created, talk to your partner and see if you can come up with a method for working out the shaded areas." Give students a little time to discuss, and then bring the class together to share their suggested methods. Then ask students to use these methods to work out all the areas for each curvy pattern.
Students might need prompting to choose a letter or value to represent the radius of the smallest semi-circle in order to work out the areas. There is scope for some discussion here about the merits of assigning a unit length rather than using a variable, and why this is 'allowed' in a question asking about proportion.
Surprisingly, each coloured region on a diagram is the same proportion of the total area. Once students have found that result, they could work on a pattern with more regions to see if the same result follows.
To prove the general case that all regions have equal area is quite challenging. A more accessible question to work on first of all is to show that the first region (coloured red in our diagrams) is always $\frac{1}{n}$ of the total area, for a shape with $n$ regions.
The diagram below builds a similar pattern from rectangles and could be used to develop appropriate arguments, without needing to include $\pi$ in calculations.

Key questions
Where are the centres of semicircles in the diagrams?
Possible support
The problem An Unusual Shape provides practice in calculating the areas of semicircles.
The problem Blue and White investigates sequences based on the areas of circles.
Possible extension
Prove algebraically that all sections have equal area for a circle with $n$ sections
