At Right Angles
Can you decide whether two lines are perpendicular or not? Can you do this without drawing them?
Problem
At Right Angles printable sheet
This problem follows on from How Steep is the Slope?
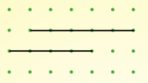
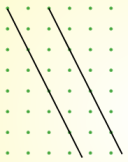
It's easy to draw parallel lines - just check that the gradients match.
Image
| Image
| Image
|
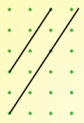
| Gradient $\frac{3}{2}$ | Gradient $0$ | Gradient $-2$ |
But I'm finding it harder to draw perpendicular lines. Here are my best efforts so far but I don't think they're quite right!
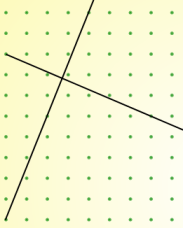
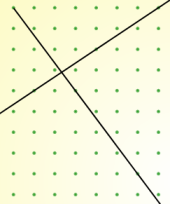
I know that the sides of a square are at right angles, so if I learn to draw tilted squares I may be able to find an efficient method for drawing perpendicular lines.
Experiment with the interactivity below until you can draw squares with confidence.
Work out the gradients of the lines which form your squares.
Is there a relationship between the gradients of perpendicular lines?
Can you use your relationship to explain why the two sets of lines above are not perpendicular?
| First line | Second line | ||||||||
| Through (6,9) and (10,1) | Through (4,2) and (14,7) | ||||||||
| Through (6,8) and (21,12) | Through (1,4) and (5,14) | ||||||||
| Through (-3,-2) and (-1,1) | Through (6,1) and (15,-5) |
Getting Started
How do you get from one vertex of a square to the next one?
How far across? How far up?
And to the next vertex? And to the next? And back to the start?
Student Solutions
A lot of people correctly identified that product of the gradients of two perpendicular lines is always -1. There were a variety of approaches to the problem:
Octavia from Melbourn Village College first established the rule and provided examples to show it worked, and then applied it to the lines in the problem
When you multiply the gradient of one line by the gradient of the other line, you get negative 1, if the lines are perpendicular. For example; look at the square. If you take the gradient of the red line, you get -1. The gradient of the blue line is 1. 1 lot of -1 is -1.
All perpendicular lines follow this rule; it always equals minus one. You can show this in a table.
| Line 1 | Line 2 | Product |
|---|---|---|
| $1$ | $-1$ | $-1$ |
| $\frac{3}{2}$ | $\frac{-2}{3}$ | -1 |
| $3$ | $\frac{-1}{3}$ | $-1$ |
The formula is $L_1=L_2\times(-1)$ e.g. take the first example. $-1\times(-1)=1$.
Does this work with the second example, Octavia?
The two sets of lines in 'At Right Angles' are not perpendicular, because when the gradients of the pairs of lines are multiplied together they do not equal -1.
Take the second example. One line is -1.333, and the other is 0.666, which multiplies to make -0.888.
The first pair of lines is perpendicular $(-2\times 0.5=-1)$
The second pair of lines is not perpendicular
The third pair of lines is perpendicular $(1.5 \times \frac{-2}{3}=-1)$
Nadia from Melbourn Village College described the relationship in a slightly different but equally valid way
For every pair of perpendicular lines one line's gradient will be $\frac{a}{b}$ and the other lines gradient will be $\frac{-b}{a}$.
Beth from Melbourn Village College provided the following very extensive solution to all the different parts of the problem
Is there a relationship between the gradients of perpendicular lines?
Yes, because if the two lines are perpendicular then one of the gradients has to be positive and the other negative. The line with the negative gradient is the inverted fraction of the positive gradient line. For example, positive gradient $\frac{1}{2}$ negative gradient -2 (also written as $\frac{-2}{1})$. In addition, each angle between the lines where they meet is a right-angle. However when the lines overlay the $x$- and $y$- axis neither of these lines are either positive or negative but they are still perpendicular.
Can you use your relationship to explain why the two sets of lines above are not perpendicular?
For the first set of lines:
The line with the positive gradient has a gradient of $\frac{3}{7}$. The line with the negative gradient has a gradient of $\frac{-5}{2}$. The second gradient is not the first one inverted, so therefore the two lines are not perpendicular.
For the second set of lines:
The line with the positive gradient has a gradient of $\frac{2}{3}$. The line with the negative gradient has a gradient of $\frac{-4}{3}$. The second gradient is not the first one inverted, so therefore the two lines are not perpendicular.
Decide whether the two lines are perpendicular or not, and explain how you know.
For the first set of lines:
In this case the line with the positive gradient has a gradient of $\frac{1}{2}$. The line with the negative gradient has a gradient of $\frac{-2}{1}$. The second gradient is thr first one inverted, so therefore the two lines are perpendicular.
For the second set of lines:
Both lines have negative gradients, one line has the gradient of $\frac{-1}{4}$ and the other $\frac{-5}{2}$, so they are not perpendicular because the second gradient is not the first one inverted and also if both lines are negative then they can't be perpendicular.
For the third set of lines:
The line with the positive gradient has a gradient of $\frac{11}{7}$. The line with the negative gradient has a gradient of $\frac{-2}{3}$. The second gradient is not the first one inverted, so therefore the two lines are not perpendicular.
Can you decide without plotting the points?
Yes, there is an equation which can help you to find out the gradient. To find the gradient of a line you do $y$ over $x$, and because there are two points you need to find the difference between the $y$-coordinates and the $x$-coordinates. The equation is $\frac{y_1-y_2}{x_1-x_2}$ this equation will give you the gradient of the line which you can then work out from if the lines are perpendicular or not. Once you have the two gradients if when you multiply them together the answer is -1, then the two lines are perpendicular.
Steve (no school listed), described an interesting method for demonstrating why the products of gradients must be -1
Draw the same line on two grids. Then rotate one by 90 degrees. This gives me two lines which are at right angles. Since the grids are square grids I know that the grids will lie on top of each other after this, so I can put the second line back on the first grid to get two perpendicular lines.
If the first line goes across $+x$ and up $+y$ from one end to the next then the second must obviously go across $-y$ and up $+x$.
The gradient of the first line will be $\frac{+y}{x}$ whereas the gradient of the second line will be $\frac{-x}{y}$. So the gradient of the first line is -1/(gradient of the second line).
Ashley from Durrington High School came up with a memorable summary of the relationship
I find that it is very easy to remember with these words; negative reciprocal. If you have $y=3x$, your perpendicular line will be $y=\frac{-1}{3}x$ and if you have $y=\frac{-2}{3}x$, then your perpendicular line is $y=\frac{3}{2}x$.
Teachers' Resources
Why do this problem?
This problem challenges students to use what they know about gradients to make general statements about the gradients of perpendicular lines.
- An exploration of Pythagoras' Theorem (see for example Tilted Squares)
- Straight line graphs (see for example Parallel Lines and Perpendicular Lines)
Possible approach
This problem follows on from How Steep is the Slope?
Introduce students to the existence of tilted squares, by playing the game Square it or using the activities Eight Hidden Squares and Ten Hidden Squares.
Hand out this 8 by 8 square dotty grid and ask students, perhaps working in pairs, to find all the different tilted squares which can be drawn with vertices at the dots. Clarify that two squares are the same if one could be cut out and placed exactly on top of the other. There are twelve different tilted squares. There is no need to share this information with the students; ideally challenge the students to justify that they have found all the possible tilted squares.
Once students have had a chance to find most of the tilted squares, ask them to report back. Agree a way of describing the squares they have found, perhaps by reference to the way you move to get from one vertex to the next. The interactivity can be used to check that the shapes identified are indeed squares. Keep a record of the squares found, perhaps in a table that can be added to later.
Once all twelve have been identified, and there is agreement that there are no more, ask students to find the gradients of adjacent sides in each square. Add this information to the table with the square descriptors.
Bring the class together to discuss what they have noticed about the gradients. Can they predict the gradient of a side of a square if they are given the gradient of the adjacent side?
Ask students to describe a method for checking whether two lines are perpendicular to each other.
Now set the task at the end of the problem where students must decide whether two lines given by their coordinates are perpendicular. Students could follow this up by making up their own sets of lines (which must contain some which are perpendicular and some which are not) and challenging their partners to identify the perpendicular ones.
Key questions
Possible support
If students are struggling to draw tilted squares, they could work at computers using the interactivity provided in the problem. They could complete squares of different sizes and list how to get from one vertex to the next. These results could be used in the next stage of the lesson.
Possible extension
This problem could be followed up by Square Coordinates and then Tilted Squares for a geometrical introduction to Pythagoras' Theorem.
Alternatively, students can move into algebra by investigating the relationship between the equations of parallel and perpendicular lines on a co-ordinate grid in Parallel Lines and Perpendicular Lines
