Flagging
Problem
How many tricolour flags are possible with 5 available colours
such that two adjacent stripes must NOT be the same colour. What
about 256 colours? 
<-- Here's an example for 3 colours.
Student Solutions
Thank you Kang Hong Joo for this solution:
Now, let the flag split into three parts. In the first part, 5 colours can be put into it. In the second part, only 4 colours can be put into it, as it cannot be the same colour as the first part. In the third part, only 4 colours can be put into it, as it cannot be the same colour as the second one yet it can be the same colour as the first one. Thus, the number of tricolour flags are 5 x 4 x 4 = 80 with 5 available colours.
If there are 256 colours, by the same reasoning, the number of tricolour flags possible are 256 x 255 x 255 = 16 646 400.
Helen Battersby Year 9 The Mount School York explained the reasoning as follows:
For 2 colours there are only 2 possible patterns.
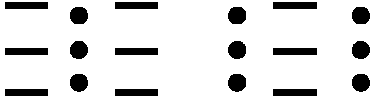
And for 3 colours there are 12, as given in the question. Rearranging the 12 solutions given into ones beginning with the same colour, I could see that each beginning had 4 different combinations. So with 3 colours the calculation is 3 x 4 = 12. Looking at 4 colours, I could see that from the logic in this, each beginning (like the dots as shown) would have 9 different combinations. There can be 4 beginnings as there are 4 colours, so altogether there are 4 x 9 = 36 flags.
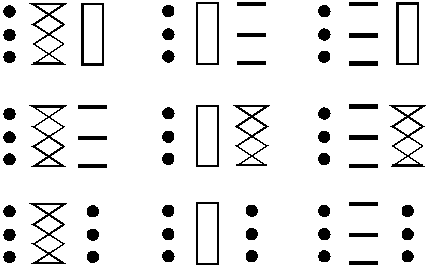
This suggests a rule$c \times (c - 1)^2$ where $c$ stands for the number of colours.
If this is right 256 colours will give 16 646 400 combinations.Well done all the following for your excellent work on Flagging: Patrick Coleman, Scott Reynolds , St Peter's College, Adelaide, Australia, Michael Swarbrick Jones , Y7 Comberton Village College, Cambridgeshire, Catherine Harrison, Joanne Barker, Rachael Evans, Sheila Luk and Cheryl Wong , Year 9 The Mount School York, P. Cresswell , City of Norwich School and James Page , Hethersett High School, Norwich.
