A chordingly
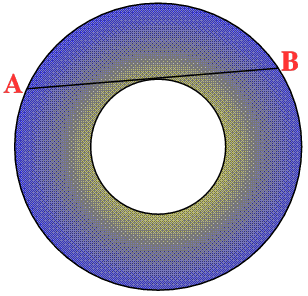
Find the area of the annulus in terms of the length of the chord
which is tangent to the inner circle.
Problem
Prove that the area of the annulus is ${1\over 4}\pi AB^2$ where
$AB$ is a tangent to the inner circle.
Image

Student Solutions
Image

Jessica Zhang of Woodbridge High School, Arwa Jamil , Year 8, the International School Brunei and Nisha Doshi and Suzanne Abbott from Year 9 the Mount School, York all sent good solutions to this problem.
Let the radius of the big circle be $R$ and the radius of the small circle be $r$. By Pythagoras theorem: $$ R^2 - r^2 = ({1\over 2}AB)^2 $$ The area of the big circle is $\pi R^2$ and the area of the small circle is $ \pi r^2 $. The area of the annulus $A$ is the area of the big circle minus the area of the small circle so: $$ A = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) = \pi({1\over 2}AB)^2 = \pi (AB)^2/4. $$
