Can They Be Equal?
Can you find rectangles where the value of the area is the same as the value of the perimeter?
Problem
Can They be Equal? printable sheet
Charlie has been drawing rectangles:
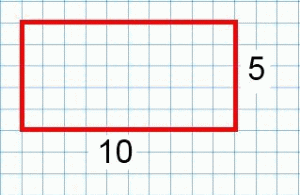
The first rectangle has a perimeter of 30 units and an area of 50 square units.
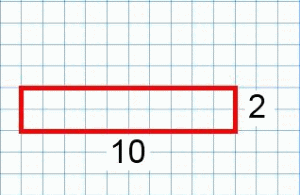
The second rectangle has a perimeter of 24 units and an area of 20 square units.
Charlie wondered if he could find a rectangle, with a side of length 10 units, whose perimeter and area have the same numerical value.
Can you find a rectangle that satisfies this condition?
Alison says "There must be lots of rectangles whose perimeter and area have the same numerical value."
Charlie is not so sure.
Can you find more examples of such rectangles?
Can you come up with a convincing argument to help Charlie and Alison decide if Alison is right?
Click here for a poster of this problem.
Getting Started
Find the dimensions of the following rectangles:
| Dimensions | Area | Perimeter |
| 9 | 20 | |
| 16 | 20 | |
| 21 | 20 | |
| 24 | 20 | |
| 25 | 20 |
Draw the rectangles.
What do you notice about the shapes of rectangles with a fixed perimeter as their areas increase?
Find the dimensions of the following rectangles:
| Dimensions | Area | Perimeter |
| 24 | 20 | |
| 24 | 22 | |
| 24 | 28 | |
| 24 | 50 |
Draw the rectangles.
What do you notice about the shapes of rectangles with a fixed area as their perimeters increase?
Student Solutions
We had lots of solutions to this problem, so well done to everyone who submitted an answer!
David, Noah, Felix, Tom, Amy and Laura from Bristol Grammar School worked on this problem together. David says:
We found that the 6 by 3 rectangle works, because 6+3+6+3=18 and 6x3=18, so this has equal area and perimeter.
Laura and Amy say:
We have been working systematically to list all the possible rectangles, e.g. 1x1 1x2 1x3 1x4 ... and deciding whether there are cases with 1, 2 or 3
3x1 3x2 3x3 3x4...
We noticed a diagonal pattern for where the perimeter becomes less than the area.
We are still working on a solution!
Well done to Gourav from India, Radha from Stanhope, Kirstey from da Vinci College and Caitlin from Marshfield Primary who all correctly found rectangles with the same area and perimeter, such as 4x4 and 3x6.
Hannah from Leicester Girls High made some good notes on even and odd numbers:
I realised that at least one of the length or the width of the rectangle has to be even. The perimeter will always be even, because the length is multiplied by 2, making it even, and is added to the width which has been multiplied by 2, also making it even. But if both the length and the width are odd, then the area will be odd, meaning that it is impossible for the perimeter to be the same as the area.
Click here to see how Dexter from Wilson's School used diagrams to understand different rectangles and how he also used some algebra to find examples of rectangles where the perimeter is equal to the area.
Lucy from Belgium noticed visually what was happening to rectangles with whole number side lengths:
Each square along the edges accounts for one unit of perimeter, except for the four corner squares. They account for two units of perimeter but only one unit of area. This means the perimeter is 4 more than the area and there will have to be some squares in the middle that will only be counted for the area and not the perimeter.
Bhavik from Queen Elizabeth's School for Boys also considered rectangles with whole number side lengths, and came to the same conclusion. Click here to see his very clear explanation of why there can only be two such rectangles where the area is equal to the perimeter.
Nathan from Rushmore Primary made an attempt at using algebra, which was continued by Vicki from Farnborough Hill, Eliza and Jacqueline from Chevalier College, Australia and Tom. Vicki noted that for a rectangle x by y, the area is equal to the perimeter if: $$ \begin{align*} xy &= 2x+2y \\ xy-2y &= 2x \\ y(x-2) &= 2x\\ y &= \frac {2x}{x-2} \end{align*} $$
Niharika then looked at the possible values of x and y from this equation: $$ \begin{align*} y &= \frac {2x}{x-2} \text{ and } x ,y> 0 \\ \Rightarrow x-2 &> 0 \\ x&> 2 \end{align*} $$ There are an infinite number of these rectangles.
Substituting in different values of x and y and checking the answers are correct is a good problem solving skill - well done to Krystof and Mimas who did this. Also Shashank from India drew a graph of the possible x and y values:
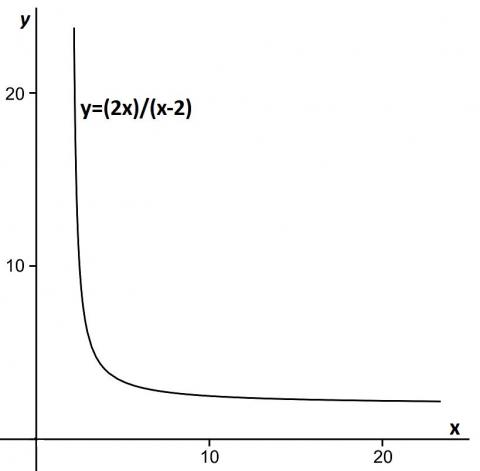
Esther commented that:
Although you can always put a number into the formula I used, $2x+2y=xy$, the end result is not always an integer.
In fact, the only rectangles like this with side lengths integers are a 3x6 rectangle and a 4x4 square.
Any other numbers substituted into the formula as x will give a decimal output for y.
For example, if you put in 5 as x, your value for y would be 10/3.
Well done to Miss Gerrard's 2BE Class from Perth High School, who noticed some interesting connections between area and perimeter:
We all found 2 rectangles that worked fairly quickly. They were the square with sides of 4 (A=P=16) and the rectangle with sides 3 and 6 (A=P=18).
Well done to you all.
Teachers' Resources
Why do this problem?
Sometimes area and perimeter of rectangles are taught separately, and are often confused. In this problem students consider the relationship between them and are being challenged to engage in some sophisticated mathematical thinking.
Possible approach
This printable worksheet may be useful: Can They Be Equal.
Show the students this image and ask them to work out the area and perimeter of each rectangle.
- fix one attribute (side length, area, perimeter) and vary the others using trial and improvement
- fix one attribute and use algebra to solve for the other attributes
- write an algebraic expression for area and perimeter, equate them, and substitute values into the resulting equation
Possible support
A more scaffolded introduction to the problem:
Possible extension
Ask students to consider other polygons with numerically equal areas and perimeters - those who have met Pythagoras' theorem could investigate right-angled and isosceles triangles, and those who have met trigonometry could work on regular polygons.
