Eight Hidden Squares
On the graph there are 28 marked points. These points all mark the vertices (corners) of eight hidden squares. Can you find the eight hidden squares?
Problem
On the graph below there are $28$ marked points.
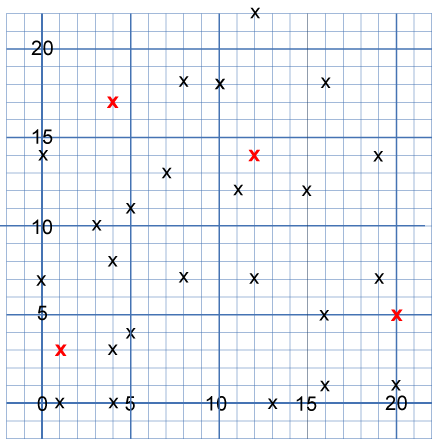
These points all mark the vertices (corners) of eight hidden squares.
Each of the $4$ red points is a vertex shared by two squares.
The other $24$ points are each a vertex of just one square.
All of the squares share just one vertex with another square.
All the squares are different sizes.
There are no marked points on the sides of any square, only at the vertices.
Can you find the eight hidden squares?
Getting Started
It would probably help to print out the problem or use this sheet.
Don't forget that some squares may be tilted!
Student Solutions
Lots of school groups handed in excellent solutions to this problem.
Well done particularly to Ramu and Atasha from Brookland Primary School for their answers:
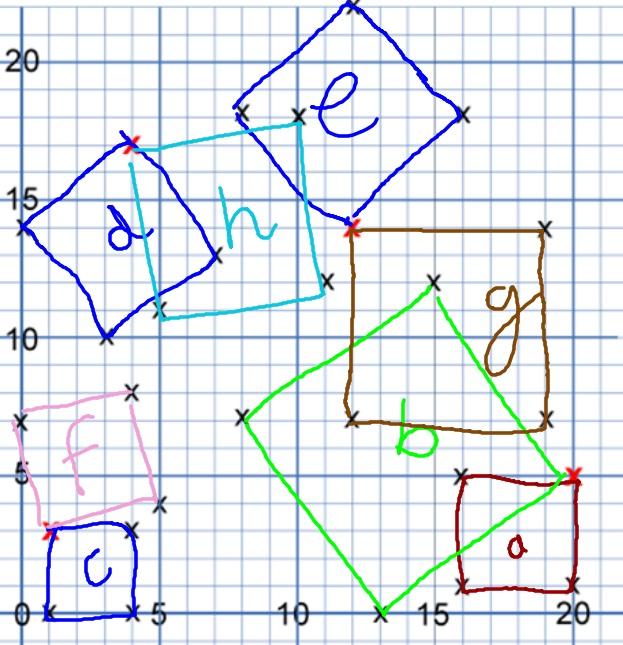
Square 1 - (1,0) , (1,3) , (4,0) , (4,3)
Square 2 - (1,3) , (0,7) , (5,4) , (4,8)
Square 3 - (20,1) , (16,1) , (16, 5) , (20,5)
Square 4 - (0, 13) , (8,7) , (20,5) , (15,12)
Square 5 - (12,7) , (12,14) , (19,7) , (19,14)
Square 6 - (12,14) , (8,18) , (12,22) , (16,18)
Sqaure 7 - (5,11) , (11,12) , (10,18) , (4,17)
Sqaure 8 - (0,14) , (3,10) , (7,13) , (4,17)
The Year 4s from Bradfield Dungworth sent in their picture:
As
As did the Year 6s from Wingrave C of E:
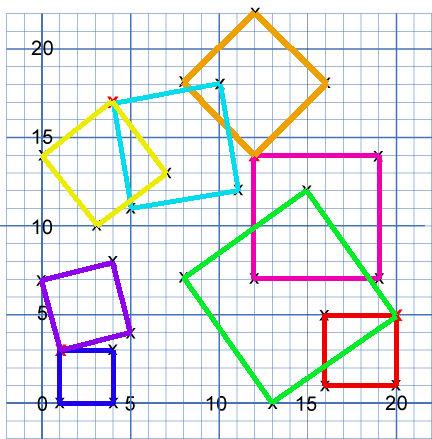
Congratulations everyone!
Teachers' Resources
Why do this problem?
This problem has two aspects. A secure knowledge of the properties of squares is required and also acquaintance with coordinates in the first quadrant.
Possible approach
This printable worksheet may be useful: Eight Hidden Squares.
You could start by drawing a square in various orientations, each time asking what shape you have drawn. Often children will say "diamond" when a square is presented diagonally. Alternatively, if the group is already familiar with squares in different orientations, you could start by drawing some shapes by giving their coordinates. This sheet could be used on an interactive whiteboard or enlarged to A3 and drawn on directly.
You could continue by choosing one point on the grid of the actual problem and then selecting a second point to form a second corner of a square. You could then ask where a third corner could be now and if there isn't a cross in the position, ask the class to suggest alternatives. Once you have found a possible third corner, ask where the fourth corner would have to be in order to make a square.
Key questions
How does that square lie on the grid?
Possible extension
Students who are familiar with coordinates in all four quadrants could try the similar problem Ten Hidden Squares instead.
Possible support
Suggest using this sheet and sketching out possible squares one at a time starting with one point and looking for others that make a square with it. It might be helpful for some children to try Complete the Square first.
