Half Past Two
Weekly Problem 21 - 2009
What is the angle between the two hands of a clock at 2.30?
What is the angle between the two hands of a clock at 2.30?
Problem
What is the angle between the two hands of a clock at 2.30?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Image
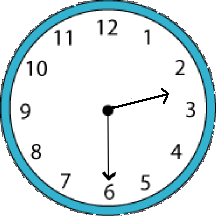
In moving from one number on the clock face to the next, a hand moves $360 \div 12 ^\circ = 30 ^\circ$.
At 2.30, the hour hand will be exactly half way between the $2$ and the $3$, and the minute hand will be exactly on the $6$.
So the angle between the two hands will be $3 \times 30^\circ + 15^\circ = 105^\circ$.
