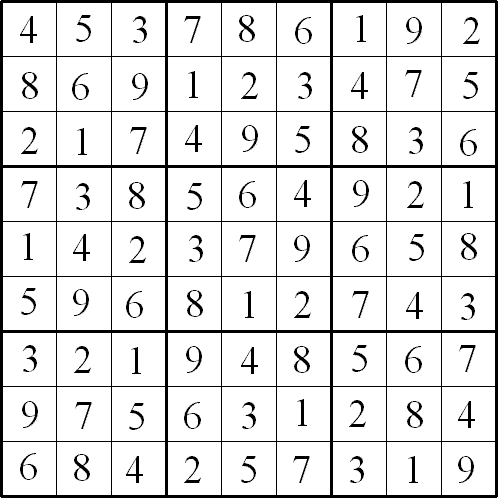
Another Quadruple Clue Sudoku
This is a variation of sudoku which contains a set of special clue-numbers. Each set of 4 small digits stands for the numbers in the four cells of the grid adjacent to this set.
Problem
By Henry Kwok
Image
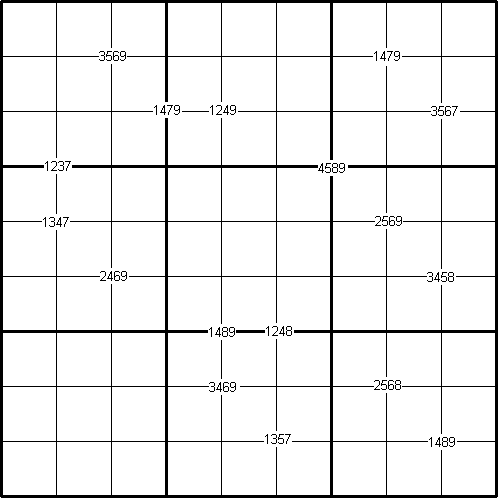
Rules of Quadruple Clue Sudoku
This is a variation of sudoku on a "standard" $9 \times 9$ grid which contains a set of special clue-numbers. These are small numbers provided by sets of $4$ small digits.
Each set of $4$ small digits in the intersection of two grid lines stands for the numbers in the four cells of the grid adjacent to this set.
The remaining rules are as in a "standard" sudoku, and the object of the puzzle is to fill in the whole $9 \times 9$ grid with numbers $1$ through $9$ so that each row, each column, and each of the nine $ 3\times 3$ boxes must contain all the nine different numbers $1$ through $9$.
For example, in the puzzle, taking the two sets of adjacent cells with small digits {$1479$} and {$3567$}, we find that they overlap at the cell with the number $7$. The rest of the puzzle is solved in the same way through logical deduction using the usual sudoku techniques and by determining the numbers in the cells in one set that overlap the cells in other sets.
Student Solutions
Image