Trice
Problem
ABCDEFGH is a 3 by 3 by 3 cube. Point P is 1/3 along AB (that is AP : PB = 1 : 2), point Q is 1/3 along GH and point R is 1/3 along ED.
What is the area of the triangle PQR? 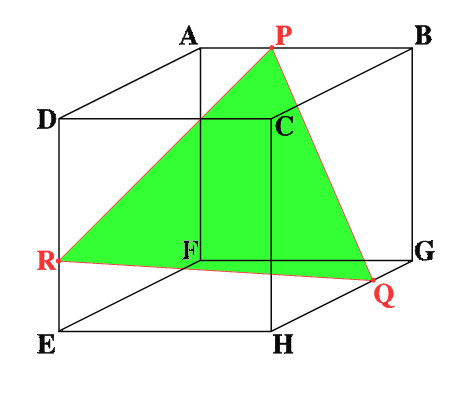
Student Solutions
ABCDEFGH is a 3 by 3 by 3 cube. Point P is 1/3 along AB (that is AP : PB = 1 : 2),
point Q is 1/3 along GH and point R is 1/3 along ED.
To find the area of the triangle PQR, Bithian Heung's solution use Pythagoras' theorem twice and shows that triangle PQR is an equilateral triangle.
$$BQ = \sqrt {BG^2+ GQ^2} = \sqrt {3^2+ 1^2} = \sqrt {10}$$
$$PQ = \sqrt {PB^2 + BQ^2} = \sqrt {2^2 + 10} = \sqrt {14}$$
Similarly $QR = RP = \sqrt {14}$ and hence PQR is an equilateral triangle.
It is useful to remember that an equilateral triangle splits into two 30-60-90 degrees triangles. By Pythagoras theorem again the ratio of the sides is 1: $\sqrt 3$ : 2.
Hence the area of the triangle PQR is $\frac {1}{2} (7\sqrt 3)$ square units.

