Investigating the dilution series

1) It is clear the highest concentration which is achievable is the original concentration of 100000 cells/ml, which results in transferring solution between subsequent beakers but without adding any additional water.

 

Image

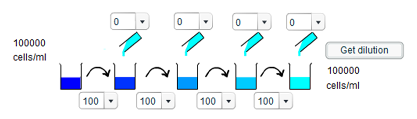
The smallest concentration results from transferring the minimum amount of solution each time (10ml) but adding the maximum amount of water (100ml). This gives a minimum final concentration of 6 cells/ml.

 

Image

2) It should be noted that for several of the required dilutions, there are more than one possible way to make them. However, only a single solution is provided below:

a) To achieve a concentration of 10 cells/ml requires a dilution of 10,000 times. Since we have four opportunities to dilute the original solution, this logically requires a tenfold dilution each time. Thus, 10ml of solution should be transferred each time, and 90ml of water added to it.

 

Image

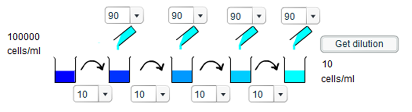
b) To give a concentration of 100 cells/ml, the same process should be repeated as in a) except that the final addition of water should not occur. Thus only three tenfold dilutions occur, and so the final concentration is 100 cells/ml as opposed to 10 cells/ml.

 

Image

c) To give a concentration of 160 cells/ml requires a 625 times dilution, which can be decomposed into a two 2.5x dilutions and two 10x dilutions. Thus, to give the required concentration involves taking 20ml of solution and adding 30ml of water, and then taking 10ml of solution and adding 90ml of water, before repeating both of these steps.

 

Image

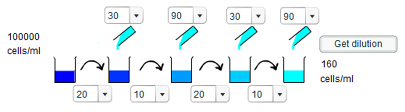
d) To achieve a 20 cells/ml concentration is similar to that of the 10 cells/ml dilution, except that the final step is different. Rather than taking 10ml of solution and adding 90ml of water to give a tenfold dilution, 20ml of solution is taken and 80ml of water adding to give a fivefold dilution.

 

Image

e) To give a concentration of 125 cells/ml requires a dilution of 800 times. This can be easily decomposed into two tenfold dilutions and one eightfold dilution. Thus, the first two dilution steps involve taking 10ml of solution and adding 90ml of water, whereas the third step involve staking 10ml of solution and adding 70ml of water. The final step involves no addition of water.

 

Image

f) A concentration of 1875 cells/ml requires a dilution of $\frac{160}{3}$. We are essentially saying that $100000 \times \frac{3}{160} = 1875$, and so require up to four fractions which multiply together to give $\frac{3}{160}$. Three such fractions are $\frac{3}{5}$, $\frac{1}{8}$ and $\frac{1}{4}$. Thus, the first dilution involves taking 30ml of solution and adding 20ml of water; the second involves taking 10ml of solution and adding 70ml of water; the third involves taking 10ml of solution and adding 30ml of water; whereas the fourth requires no addition of water.

 

Image

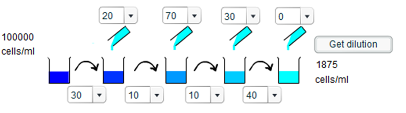
3) At each dilution stage it is possible to transfer between 10 and 100ml of solution (in 10ml intervals) and then add between 0 and 100ml (in 10ml intervals) of water. This gives a possibility of 110 different combinations, but unfortunately these are not all unique dilutions. For example, taking 10ml of solution and adding 10ml of water will give the same dilution as taking 20ml of solution and adding 20ml of water. By looking carefully at all these different dilutions (by writing them out!) it can be deduced that there are 64 different unique dilutions possible.

4) A dilution of 1/11 can be made very simply: just take 10ml of solution and add 100ml of water. However a dilution of 1/17 is impossible to make in a single dilution since no less than 10ml of solution can be taken, and no more than 100ml of water can be added. We can get a denominator of 17 by taking 100ml of solution and 70ml of water - this would give a dilution 10/17 of the original. Then we need to do a tenfold dilution to get 1/17; we can do this by taking 10ml of solution and adding 90ml of water. 

To get a 1/23 dilution we would need to make a fraction with 23 in the denominator. This will not be possible since the denominator is made by adding the amount of solution to the amount of water (and dividing by 10 since we are using multiples of 10ml throughout), so the maximum denominator in a single step is achieved by adding 100ml and 90ml, giving a denominator of 190 which cancels to 19. We can't make a denominator of 23 in more than one step since 23 is prime, and each subsequent step multiplies the denominators together.

5) A dilution of 1/21 can be made by recognising that the fraction can be written as a product of 1/3 and 1/7. Thus, using two dilutions 1/21 can be made: firstly take 10ml of solution and add 20ml of water. Next, take 10ml of this new solution and add 60ml of water.

A dilution of 1/46 cannot be made exactly. 1/46 can be decomposed to 1/2 x 1/23. Although a dilution of 1/2 can be made, it is not possible to then dilute this by a factor of 23. 

6) Dilutions cannot be made for fractions whose denominators are prime numbers greater than 19, or multiples thereof. With the added restriction of only performing four dilutions altogether, to decide whether a particular dilution is possible it is necessary to consider how to express the fraction as a product of those fractions which can be made in one dilution.