Tiling
Problem
Let's imagine we are tiling a floor or patio area.
Suppose the area is square and is 3 by 3.
Tiles come in three sizes: 1 by 1, 2 by 2 and 3 by 3.
You are allowed to use any arrangement of these tiles to cover the space completely.
However, none of the tiles can be cut.
For this challenge, we are interested in the total number of tiles you use for any arrangement.
For example, for the 3 by 3 square you could do it by using:

Therefore the smallest number of tiles is one and the largest is nine and the only other value you can get between one and nine is six (using one 2 by 2, and five 1 by 1).
Now imagine you also have tiles which are 4 by 4 in size.
What total numbers of tiles can you use for a square patio that is 4 by 4?
If you could have tiles which are 5 by 5 as well, what total numbers of tiles can you use for a square patio that is 5 by 5?
The final part of this activity is to examine carefully the answers you get for each of the three sizes of floors - 3 by 3, 4 by 4 and 5 by 5.
Now talk about and record what you notice.
Make some statements about what you therefore think will happen if someone takes the long time needed to explore a 6 by 6 and 7 by 7 square.
Getting Started
What is the largest number of tiles you can use? How?
Student Solutions
Alex, Ayali, Brodie and Keya from Strand on the Green Primary School sent the following:
We decided the easiest way was to start with the biggest tiles that could fit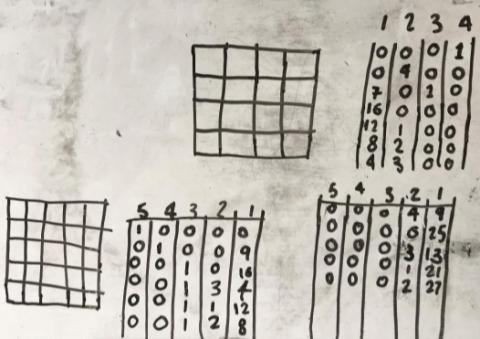
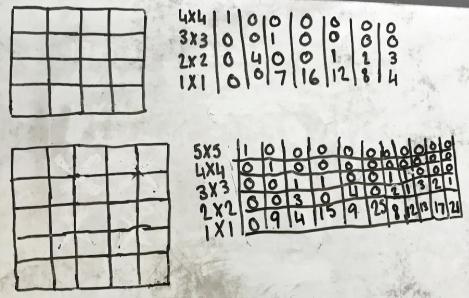
We agreed there are 7 possibilities for the 4 by 4 square and 11 for the 5 by 5 square. Initially that looks like a sequence adding 4 each time. However there are already 7 possible totals for the 6 by 6 square using the 6x6, 5x5 and 4x4 tiles so there will definitely be more than 15 (but we didn't have time to find them all).
Students from the International School of Brussels sent in their work: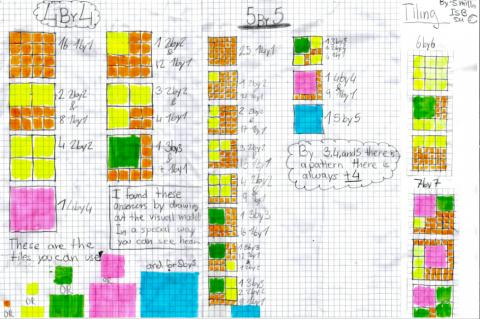
So, both submissions thought that the +4 from one size to another was a particular point of interest and maybe a rule?
Well done both sets of pupils.
