New House
Problem
Well it's nice to move into a new house sometimes. For some people it's great fun to design and make a new house. I've been thinking of an idea where the house is built out of blocks which are the rooms. I don't know whether you've seen some builders' sheds set up this way on big building sites when the sheds or offices are linked together with big steel girders? Well I'm thinking that it could be good fun to design houses with that sort of idea in mind.
Well we have to buy some land first and suppose that we buy four big squares.
I reckon that a good house may have about 7 rooms. So let's use some interlocking cubes to stand for the rooms and arrange each of them so that they are connected and NOT spilling over the 4 square base size.
Perhaps like this - I've used 7 differently coloured cubes so as to follow things more easily:-

There are of course lots of different designs.
Take some interlocking cubes such as "multilink" and have a go at making some now!

But according to what your interlocking cubes are like you may or may not be able to do that one.
But maybe you could do:-

The whole idea of this investigation is to try to find all the different designs that you can. You can decide for yourselves whether shapes that are just turned around $90^\circ$ are the same or different. The same goes for the designs that are reflections of another design.
YOU DECIDE.
It would probably be good to see if you can find some kind of system/method/pattern for doing these and try to write down those ideas that you have.
Of course we have to ask "I wonder what would happen if ...":a/ the base was 5, 6, 7, 8, or 9 squares?
b/ the base was bigger, would it matter what shape the squares are arranged in?
c/ you had 8 or 9 or 10 rooms?
d/ etc.
Here is some dotty isometric paper which might help for drawing the cubes.
If you're not sure about drawing them on these dots it really does not matter. But if you fancy that idea and you have not used these triangular arranged dots before then this is what you do:
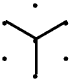
1/ Take 7 dots arranged like a hexagon with one dot in the middle:-

2/ Draw a capital Y by using every other dot:-
3/ Draw in the six sides of the hexagon:-
Good luck
Remember to send in your results.
Student Solutions
From the same pupils at West Flegg came some Houses ideas.
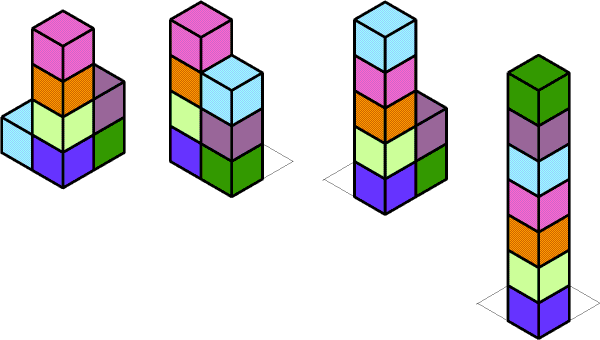
These came from Rachel. Some others came but I was unable to get them put onto the computer in a good way.
I liked these ideas Rachel, and as you say they are just a few of many ideas. If you have more, then do get in touch. Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried.
Teachers - you might like to send in a summary of your children's work.
Teachers' Resources
Why do this problem?
Possible approach

and then various ways have been found for tackling the overhanging, balcony rooms.
