Harmonically
Is it true that a large integer m can be taken such that: 1 + 1/2 +
1/3 + ... +1/m > 100 ?
Problem
(a) Is it true that a large value of $n$ can be found such that: $$S_n = 1 +{1\over 2} + {1\over 3} + {1\over 4} + ... + {1\over n} > 100?$$
(b) By considering the area under the graph of $y = {1\over x}$ between $a ={1\over n}$ and $b = {1\over n-1}$ show that this series grows like $\log n$.
Getting Started
(a) This is a divergent series, which means that the sum grows to infinitiy. To show this, consider splitting the terms to be added together into small chunks, each twice as long as the previous one
$$
(1), (2,3), (4, 5, 6, 7), (8,9,10,11,12,13,14,15) \mbox{ etc}
$$
That is add the 'chunk' of the 2nd and 3rd terms, add the'chunk' of the 4th, 5th, 6th and 7th, etc. etc.
(b) You have to show that $$S_{n-1} > \log n > S_n - 1$$ so that, for large $n$, $S_n$ is approximately equal to $\log n$.
Student Solutions
The Harmonic Series.
Murat Aygen from Turkey sent this solution to part (a) and Dapeng Wang from Claremont Fan Court School, Guildford sent in essentially the same solution.
Let us partition the terms of our series, starting from every $k= 2^{i-1}+ 1$, as follows: $\sum_{k=1}^{2^r} \left({1\over{k}}\right) = 1 + \left({1\over{2}}\right) + \left({1\over{3}} + {1\over{4}}\right) + \left({1\over{5}} + {1\over{6}} + {1\over{7}} + {1\over{8}}\right) + \sum_{i=4}^{r} \left(\frac{1}{2^{i-1}+1} + \dots + {1\over2^{i}}\right)$
How many terms are there in each partition? We see that there are 1, 2, 4, 8, 16... terms in the successive partitions given by $2^i - 2^{i -1}$ where $2^i - 2^{i -1} = 2^{i -1}(2-1) = 2^{i -1}$.
The smallest term in a partition is clearly the rightmost term ${1\over 2^i}$. This smallest term multiplied by the number of terms in the partition is equal to $${1\over 2^i}\times 2^{i -1} = {1\over 2}$$ which is always less than the sum of the terms of the partition. Anyway it is a positive constant! Since the number of terms in the series is as many as one wishes, we can form as many partitions as we wish whose partial sums are not less than 1/2. For reaching a sum of 100 only 200 partitions are needed.
Noah and Ariya from The British School of Boston, USA and Aled from King Edward VI Camp Hill School for Boys sent excellent solutions to part (b) .
Image
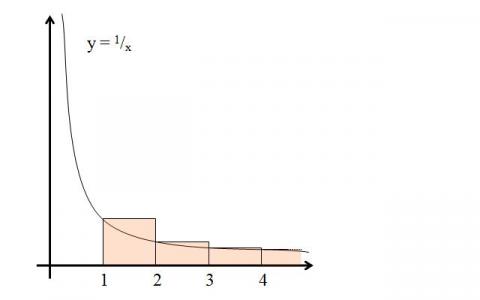
Each of the areas of the pink rectangles is representative of one fraction in the sum
$$S_n = 1 +{1\over 2} + {1\over 3} + {1\over 4} + ... + {1\over n}. $$This is verified by knowing that each rectangle x has a base of length 1 and a height of length 1/x. Every rectangle has an area greater than that under the curve $y=1/x$ it overlaps, as illustrated above (note that this will remain so because the function $y= 1/x$ is monotonic for positive numbers).
Image
|
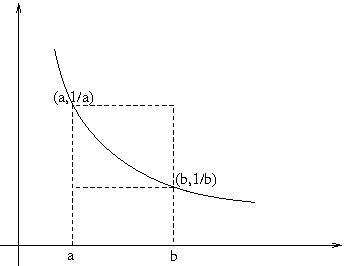
Consider the area under the graph $y = 1/x$ between $x=a$ and $x=b$. This area lies between two rectangles and so we get $${b-a \over b} < \int_a^b{ 1\over x }dx = \ln b - \ln a < { b-a\over a}$$
If we evaluate the expression between $a = {1\over n}$ and $b= {1 \over {n-1}}$ we get:
|
$${1\over n} < \ln {1 \over {n-1}} - \ln {1 \over n} = \ln n - \ln (n-1) < { 1\over n-1}$$
and this gives:
$${1 \over 2} < \ln 2- \ln 1< { 1\over 1}$$
$${1 \over 3} < \ln 3- \ln 2< { 1\over 2}$$
$${1 \over 4} < \ln 4- \ln 3< { 1\over 3}$$
...and so on
$${1 \over n} < \ln n- \ln (n-1)< { 1\over n-1}$$
Summing these expressions (noting that $\ln1 = 0$) we get:
$${1\over 2} + {1\over 3} + {1\over 4} + ... + {1\over n} < \ln n < 1 + {1\over 2} + {1\over 3} + {1\over 4} + ... + {1\over n-1} .$$
The series on each side of this inequality grow infinitely large and differ by less than 1 so the series grows like $\ln n$.
Teachers' Resources
Why do this problem?
With a hint about taking partitions of 1, 2, 4, 8 ... terms, learners can discover that, unlikely as it may seem, although the terms of the series get smaller and smaller, the sum of the series grows to infinity.
The second part requires viewing the series as a sum of areas of rectangles of unit width under the graph of $y={1\over x}$ and doing this will reinforce the basic ideas of integration.
Possible approach
Make this a class effort and encourage discussion? Ask what they think will happen to the series? Do they think the sum can grow very big? By asking the key questions below the teacher can help the class to investigate this important series.
The second part of the question could also be done by the class working together and discussing the connection between the sum of the series and the integral.
Key questions
What is the smallest term in each partition?
Can you find a lower bound for the sum of each partition?
How many partitions are needed to get a sum greater than 10?
What will the last term of the series be with this number of partitions?
Now what about a sum greater than 100?
Possible extension
Overarch
