Simultaneous equations Sudoku
Solve the equations to identify the clue numbers in this Sudoku problem.
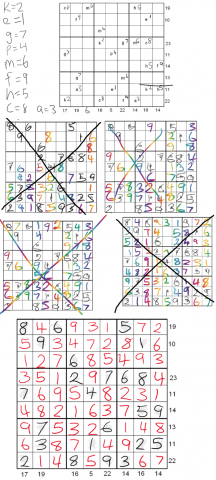
Problem
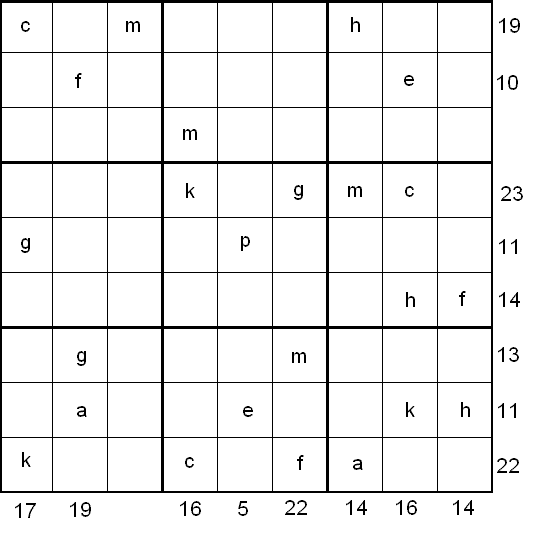
Rules of Equation Sudoku
- Each column, each row and each box (3x3 subgrid) must have the numbers 1 through 9.
- No column, row or box can have two squares with the same number.
- The puzzle can be solved by finding the values of the 9 given variables in the squares of the 9x9 grid. At the bottom and right side of the 9x9 grid are numbers, each of which is the sum of a column or row of variables. Altogether a set of 16 equations can be formed from the columns and rows of variables and constants.
You might like to start by considering the $4^{\text {th}}$ row and $4^{\text {th}}$ column.
After solving all the equations, the puzzle is solved by the usual sudoku technique and strategy.
Getting Started
Caitlin kept a record of the order in which she filled the Sudoku.
She filled the cell marked 1 first, then the cell marked 2, then the cell marked 3...
You might like to retrace her route to fill in the cells in the same order, though this is just one possible route through the problem.
You can print her journey here.
Student Solutions
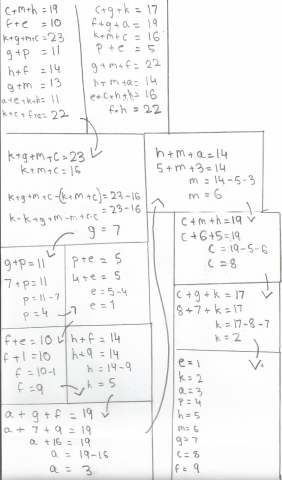
In the third row up, $g$ must be $7$ as $13-6=7.$
In the fifth row, $p$ must be $4$ since $11-7=4.$
In the sixth column, $f$ is $9$ since $22-13=9.$
In the second row, $e$ must be $1$ because $10-9=1.$
In the sixth row, $h$ is $5$ since $14-9=5.$
In the first row, $c$ is $8$ because $19-11=8.$
In the first column, $k$ must be $2$ as $17-15=2.$
By process of elimination, $a$ must be $3,$ but with this information you could easily work that out.
1st Step: Find the values of the variables in the sudoku.
Since $g + m = 13$ and $g + m + f = 22,$ therefore $13 + f = 22$ and $f = 9.$
Since $f = 9$ and $f + h = 14,$ therefore $h = 5.$
Since $f = 9$ and $f + e = 10,$ therefore $e = 1.$
Since $e = 1$ and $p + e = 5,$ therefore $p = 4.$
Since $p = 4$ and $g + p = 11,$ therefore $g = 7.$
Since $f = 9, g = 7$ and $f + g + a = 19,$ therefore $a = 3.$
Since $g = 7$ and $g + m = 13,$ therefore $m = 6.$
Since $m = 6, h = 5$ and $c + m + h = 19,$ therefore $c = 8.$
Since $c = 8, g = 7$ and $c + g + k = 17,$ therefore $k = 2.$
2nd Step: Solve the sudoku.
After finding out what the variables represent, draw up a grid and write the numbers (that you have found) in the place of the variables. This should make it easier to solve the sudoku. Now there's the usual sudoku that you can solve. I solved mine by filling out all the 6's first, then gradually worked down the possibilities of where the numbers can go.