The Old Goats
A rectangular field has two posts with a ring on top of each post. There are two quarrelsome goats and plenty of ropes which you can tie to their collars. How can you secure them so they can't fight each other but can reach every corner of the field?
Problem
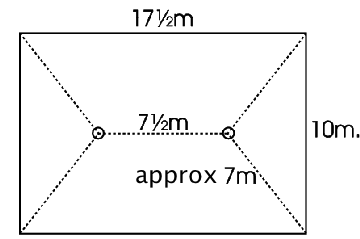
A rectangular field measuring 17.5 metres by 10 metres has two posts 7.5 metres apart with a ring on top of each post. The posts are approximately 7 metres from the nearest corners as shown in the diagram. You have two quarrelsome goats and plenty of ropes which you can tie to their collars and you want them to be able to graze the whole field between them. How can you secure them, using the posts, so they can't fight each other, and how much rope is needed?
Student Solutions
This solution came from Helen of Madras College who knew what to do with the goats:
The solution would be to get one piece of rope 15 metres long, loop it through the rings and attach the goats to either end of the rope. The goats could reach every corner of the field without difficulty. The worst that could happen would be that their horns are just touching. The rope slides through the rings at the top of the posts so at some point one goat may have only 1 metre of space whilst the other may have 14 metres. They will never be close enough to fight though. (Helen means circles of diameters 1 metre and 14 metres)
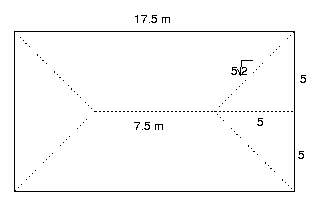
With this arrangement the goats will be pulling on each other which is enough to make even the gentlest old goat irritable! To check that the goats really can reach the corners of the field, using Pythagoras theorem you find the exact distance from the centre of the post to the corner is 5$\sqrt 2$ m which is between 7m and 7.1m. Using a single rope 14.6m long which is threaded through both the rings on the tops of the posts and tied to the collars on the goats, each goat can reach the corner of the field at his end but only when the other goat is right up against the other post. The goats can graze overlapping circles of radius 7.1m.The nearest they can get to each other is along the centre line when they are always at least 0.4 metres apart.
For the goats to be able to meet the rope would have to be at least 15m long so if the rope is between 14.6 and 15 metres the problem is solved.
