One of Thirty-six
Can you find the chosen number from the grid using the clues?
Problem
Can you find the chosen number from this square using the clues below?
1. The number is odd.
2. It is a multiple of three.
3. It is smaller than $7\times 4$.
4. Its tens digit is even.
5. It is the greater of the two possibilities.
You might like to print off this sheet of the problem.
Click here for a poster of this problem.
Getting Started
You might read through all the information first. Which statement is most useful to start with?
How about crossing out numbers or circling numbers as you use each piece of information?
Student Solutions
We had so many well-explained solutions to this problem - thank you all very much.
Adeline told us:
According to the first and second statements the only possibilities are 3, 9, 15, 21, 27 and 33.
If the third statement then says that it is smaller than 28 (7x4) then the remaining numbers off the list are 3, 9, 15, 21 and 27.
It then says that the tens digit has to be even so then the numbers 3 and 9 are immediately scraped off (because they don't have a tens digit!) leaving 15, 21 and 27. 15 has the tens digit 1 which is not even leaving the only two possibilities 21 and 27.
The last statement then says it is the bigger of the two and that is 27. So the number is 27.
Kaitlyn from Mason Middle School made a table to help her:
The answer is 27. I know this because I used the process of elimination with the given hints. The way I did this was:
| Hint | Possible numbers |
| The number is odd | 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35 |
| The number is a multiple of three | 3,9,15,21,27,33 |
| It is smaller than 7x4 (=28) | 3,9,15,21,27 |
| The tens digit is even | 21,27 |
| It is the greater of the two possibilities | 27 because that is greater than 21 |
Dylan from Oakland Township Elementary used a similar method, but he explains how he used the number grid itself to write on:
The clues 1 and 2 were the easiest to figure out. For clue 1, I circled all the odd numbers. Odd numbers are the numbers that multiples of two never touch.
For clue 2, I took all the multiples of three and circled them and crossed off the other odd numbers. Multiples of three are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, and 36. It is like counting by threes.
When clue number 3 came on, it stumped me for about 10 seconds. Then I found a different way of doing it. I decided to read clue 4 and come back to clue 3. I crossed off all the numbers with an odd number or no number for their tens.
I went to 7x4 and figured out that it is 28. I crossed off all the numbers bigger than 28.
Thank you, Dylan. Crossing out or circling the numbers as you go along can help you keep track of what you're doing. Daniel from Engelfield Green Infants School did this too. Here is what Daniel wrote:
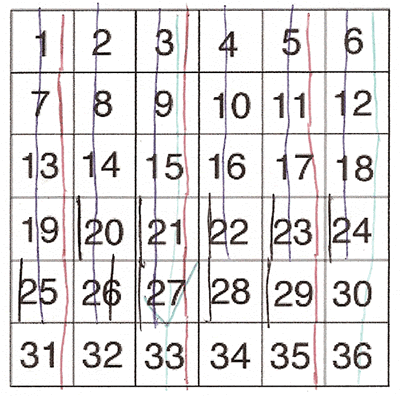
I printed off the square with the numbers.
I put a red line through all the squares with odd numbers.
I put a green line through all the squares with numbers that were multiples of three.
I put a blue line through all the squares with numbers that were smaller than 28 (7 x 4).
I put a black line through all the squares with numbers where the tens digit was even.
Here is a picture of Daniel's work:
Thank you again for all your contributions to this problem. I'm afraid there are too many to mention you all!
Teachers' Resources
Why do this problem?
Possible approach
You could then look at this problem all together and ask pairs of children to try and solve it. Emphasise that after a specified length of time you will be asking them HOW they went about solving it rather than just wanting to know the answer. It would be useful for each pair to have a copy of the problem - you could print off this sheet. It might be worth stopping them after just a few minutes to share good ways of keeping track of what they're doing. Some children might suggest crossing out or circling numbers on the grid, for example.
Once the children have worked on this problem (and possibly the extension too), the key point to bring out in a whole class discussion is the idea that the first clue was not necessarily the most useful to start with. Invite pairs to describe how they found the solution, emphasising where choices were made as to which clue they used next.
Key questions
Possible extension
Possible support
