Triangle relations
Problem
Here is an isosceles triangle and an equilateral triangle:
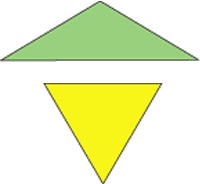
You will need to print off and cut out the two triangles to try this problem. (Here is a sheet of them which you could print off.)
What do the two triangles have in common?
How are they related?
Getting Started
You might want to measure, or fold, or cut, or draw round, or ... (or maybe all of these!).
Student Solutions
Inceeya from Glenarm College told us:
My solution is that the side of the isoceles triangle is the same length as the base of the equilateral triangle.Well noticed, Inceeya. Yes, we could say that the sides of the equilateral triangle (which of course are all the same) are the same length as the shorter sides of the isosceles triangle.
Rhea from Mason Middle School compared the triangles very thoroughly. Here are some of the things she noticed:
1. They both have three sides/three angles.
2. Both have at least two acute angles.
3. All of their interior angles add up to 180 degrees.
4. These specific triangles have no 90 degree angles.
5. They are both 2D figures.
6. These two share the same area.
Some of these things would apply to any triangles - you might like to think about which ones - and some apply just to these two triangles. Rhea told us that she cut out both the triangles and put them next to each other to make her list. I am particularly impressed that Rhea suggests they have the same area. She explained how she worked this out:
I cut the equilateral triangle in half and saw if it would fit in the isosceles triangle. To my revelation it did. This is how I established that these two triangles have an equivalent area.
Excellent - thank you to Rhea and Inceeya.
Teachers' Resources
Why do this problem?
The beauty of this problem is that it is completely open and therefore gives children the opportunity to approach it however they like. It is a great chance for you to observe and assess what they do, having conversations as you walk around the class.Possible approach
It might be appropriate for children to work in pairs or small groups and they will almost certainly need a cut-out copy of each triangle. (Here is a sheet of triangles which you could use.) It would be great to have other resources available for them to use should they want - for example rulers, pencils, squared paper, triangular dotty paper etc.Pupils will come up with a variety of different findings which might relate to side lengths, area, symmetry ... For example, some children might notice that you can halve each triangle to make two smaller triangles. The resulting four smaller triangles are in fact identical. Other children might notice that the area of each triangle is the same. You might want to bring out the fact that some of the things the triangles have in common could be exemplified in different ways.
