Star gazing
Problem
Find the ratio of the outer shaded area to the inner area for a six pointed star and the eight pointed star.
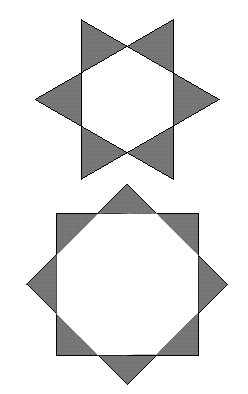
Student Solutions
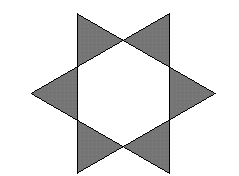
Ned, who has just left Christ Church Cathedral School in Oxford, sent a nice solution saying that: ``The Star Gazing problem is easy. The 6-point star is made up of 6 equilateral triangles, and so is the hexagon inside it, so the ratio of the `points' to the `inside' is 1:1''.
Ned then found the area of the octagon by dividing it up (a square, 4 rectangles and 4 triangles) and used Pythagoras theorem to find the lengths needed and finally found the ratio of the areas of the `points' to the `octagon inside' to be 1: (1 + $\sqrt 2$).
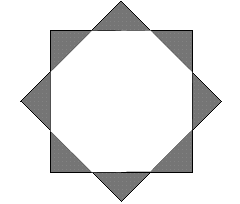
The second part is most easily done by taking the shorter sides of the triangles which make up the star to have length 1 unit, so that the area of each triangle is 1/2 and the total area of the `points' is 4 square units . The hypotenuse of each triangle has length$\sqrt 2$ (by Pythagoras Theorem) which gives the lengths of the edges of the octagon. To find the area of the octagon take the square and chop off four triangles at the corners.
The length of the side of the square is (2 + $\sqrt 2$)
the area of the octagon = (2 + $\sqrt 2)^2$ - 2
which simplifies to 4 + 4$\sqrt 2$.
Finally the ratio of areas is 4 : (4 + 4$\sqrt 2$) which simplifies to 1 : (1 + $\sqrt 2$ ).
