More building with cubes
Problem
Before you try this problem, you may like to have a go at Building with Cubes .
A. Imagine you have seven cubes. They are green, white, brown, pink, yellow, blue, and red:

Now, try to picture making this building in your head:
Start with the blue and yellow cubes. Put them next to each other.
The blue cube is on the left. It is underneath a pink cube. Put the red cube just behind the yellow cube.
Put the green cube on top of the red cube.
Put the brown cube on the right of the yellow cube.
Put the white cube in front of the pink cube.
What does your building look like?
Try using cubes to check whether you had pictured it correctly.
B. Now imagine making a building with these eight cubes:

Start with three cubes in a row.
The centre cube is pink.
The blue cube is on the right of the pink cube.
The orange cube is on the left of the pink cube.
The blue cube is also underneath a yellow cube.
Finally, put the white cube on top of the orange cube.
What does your building look like?
C. Now try imagining a building with these ten cubes:
Start with three cubes in a column.
The bottom cube is brown and the centre cube is blue.
The cube at the top is black.
Put the yellow cube underneath the red cube and put them both on the left hand side of the column of three cubes.
Rotate all five cubes a quarter turn anti-clockwise, keeping the columns pointing upwards.
Now put the dark green cube on the right of the yellow cube.
Put the white cube on the left of the brown cube and the pink cube on the left of the blue cube.
Put the light green cube on top of the black cube.
Rotate the whole building of nine cubes another quarter turn anti-clockwise (again keeping the columns vertical).
Finally, put the orange cube in front of the white cube.
What does your building look like?
Once again, try using cubes to check whether you had pictured it correctly.
We would love to receive pictures or photographs of your buildings.
Getting Started
Student Solutions
Abbie, Kyle and Sophie from Lillington Primary School sent us pictures of building A. Here is Abbie's:
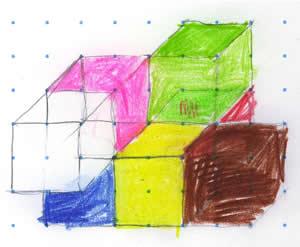
This is Kyle's:
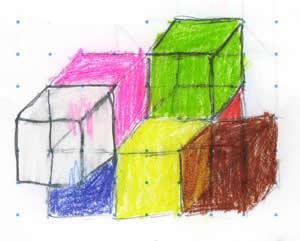
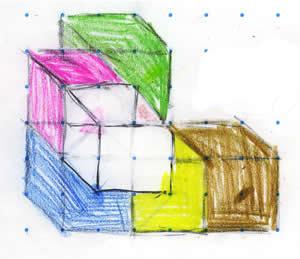
And this is Sophie's image which is drawn from a slightly different perspective:
Alice from the Royal School sent us a picture of building B, which she drew on isometric paper (a very good idea!):
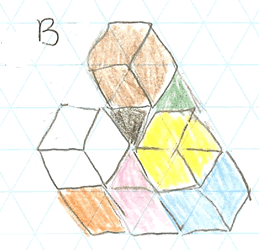
Thank you, Alice.
Pupils at Lillington Primary School also tried building C. Here is Abbie's picture:
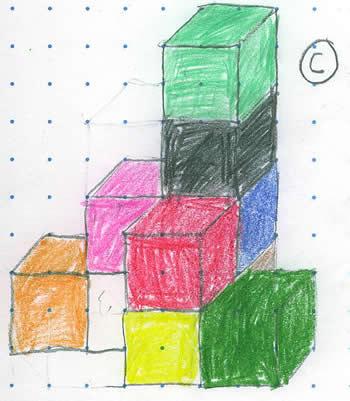
Jerrold drew it from a different perspective. Which cube can't you see? Where would it be?

Thank you, too, to Nisar, Dereece, Kyle and Sophie who all sent in pictures of building C from different angles. You must have worked hard on this activity!
