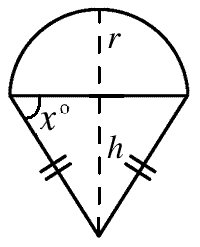
Ice Cream Tangent
The diagram shows a semi-circle and an isosceles triangle which have equal areas. What is the value of tan x?
Problem
The diagram shows a semi-circle and an isosceles triangle which have equal areas.
What is the value of $\tan x^{\circ}$?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Let the radius of the circle be r and let the perpendicular height of the triangle be h.
$\tan x^{\circ}= h/r$
Now, the area of the semicircle = ${1\over2}\pi r^2$ and the area of the triangle = ${1\over2}\times 2r \times h$
Which gives $r h$ = ${1\over2}\pi r^2$, so ${h\over r} = {\pi \over 2}$
Image