Square Bisection
Weekly Problem 8 - 2008
In how many ways can a square be cut in half using a single straight line cut?
In how many ways can a square be cut in half using a single straight line cut?
Problem
In how many ways can a square be cut in half using a single straight line cut?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Any line which passes though the centre of the square divides the square into two congruent shapes. An example is shown below.
Image
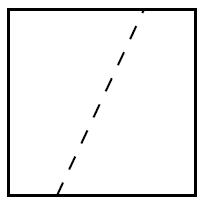
There are an infinite number of suitable lines (lines passing through the centre, at any angle) so there are infinitely many ways the square can be cut in half with a single straight cut.
