Using non-standard problems to challenge pre-conceptions
Using non-standard problems to challenge pre-conceptions: can they extend knowledge?
Jenni Back, Jennifer Piggott and Liz Pumfrey.
Primary Mathematics Project, Faculty of Education, University of Cambridge.
This paper will explore the value of using problems as a way of challenging children's mathematical pre-conceptions and explore their potential for extending their knowledge and understanding. It will do this by considering some non-standard problems taken from the NRICH website (www.nrich.maths.org) and by considering children's responses to them. The value of such problems will be examined in the light of what children have said, or implied, about their thinking by examining their solutions.On the NRICH website we offer a variety of resources for children and teachers to enrich children's mathematical experiences. These include open ended investigations, problems, games, activities and articles, some of which involve an interactive component. New problems are posted on the website nine times a year and we post solutions to the problems that children send in. This opportunity for students to present their work to an interested audience gives us feedback on what some children make of our problems, their strategies for solving them as well as some indications of the preconceptions, knowledge and understanding they bring to them.
For the purposes of this paper we will take a problem that we have presented on the website and examine the rationale for using it as well as what some of the solutions that we have received tell us about children's responses to the problem. The problem is on number but many other topics are covered on the site.
The following question has Content Level 2 and Challenge Level 1. This means it requires knowledge of curriculum content usually met by the age of 12 years and will be challenging for the "average" pupil. The focus is on non-standard problems that encourage children to think mathematically and to bring aspects of their mathematical knowledge and understanding to bear in an unfamiliar context. This question considers the relationship between prime and square numbers in a novel context:
The Problem
Two Primes Make One Square (
http://www.nrich.maths.org/public/viewer.php?obj_id=1150'??=index&refpage=freesearch.php
).
Image
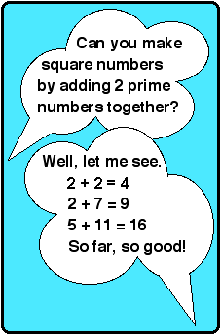
- Try with the squares of the numbers between 4 and 20.
- Did you find any square numbers which cannot be made by adding two prime numbers together?
The Rationale
The initial focus in this question seems to be the question in
the bubble in the blue rectangle. Taken from this starting point,
the problem is challenging for children as it asks them to explore
a connection that they have probably not thought of:
What is the relationship between prime numbers and square
numbers? Is there any link?
This making of connections is widely considered to be an
essential component of effective learning and teaching of
mathematics. (Askew, Brown et al. 1997) The question (to the side)
offers the potential to make the problem accessible to a wider
audience by including some calculation practice as a preliminary
task and offering a way into the problem that provides information
for the main activity. This creates a much stronger motivation for
the children than simply finding the square and prime
numbers.
Anne Watson (2002) suggests that one of the most efficient
ways of getting learners to extend their "example spaces" is by
imposing constraints. These example spaces are the set of examples
that individuals can call to mind when working on known concepts.
In relation to this problem we would suggest that simply getting
pupils to find square numbers or prime numbers does not help to
develop their understanding of the nature of either as much as this
juxtaposition to the two. The "can you make" question offers a
restriction that challenges thinking and so helps them to extend
their example spaces.
The question in the bubble combines the separate ideas about
square numbers and prime numbers into a single context, inviting
students to make mathematical connections.
The Solution
We received a number of good solutions and posted the
following answer on the website:
This question has been very well answered - thank you to everyone who sent us solutions.
D, J and M from Year 5 and B, H and He from Year 4 at St. Nicolas CE Junior School, Newbury explain how they tackled it:
"We listed the prime numbers up to 100 and then we listed the squares of the numbers between 4 and 20. Then we started working out the answers by adding two prime numbers together to make the squares until we reached 400. We found out that two squares were impossible to make. When we had an odd square number, we had to have a number that adds on to 2 to make the square number and sometimes this number wouldn't be prime. For example, to make 121 with two primes, one of the primes has to be 2, and 119 is not prime.
Our results were:
| 25 = 2 + 23 | 36 = 13 + 23 | 49 = 2 + 47 | 64 = 17 + 47 |
| 81 = 2 + 79 | 100 = 3 + 97 | 121 impossible | 144 = 47 + 97 |
| 169 + 2 167 | 196 = 29 + 167 | 225 = 2 + 223 | 256 = 89 + 167 |
| 289 impossible | 324 = 101 + 223 | 361 = 2 + 359 | 400 = 41 + 359 |
Once the calculation is done, the thinking starts. How can we
make the numbers by adding two prime numbers together? Are the
solutions presented here the only possible option in every case?
With the odd numbers, the solution has to involve 2 and another odd
number. Why?
It may be obvious to us that two is the only even prime and
that two odds added together make an even number every time but
children may not be fully aware of this information or have it as
part of their repertoire of problem solving skills.
This solution shows evidence of a child engaging with some
sophisticated reasoning about the relative sizes of numbers, the
digits involved in their construction, and the ways in which they
can be ordered. We would like to suggest that this is the product
of a non-standard problem that offers a real challenge and involves
mathematical thinking to reach a solution. Taking John Mason and
Anne Watson's (1998) descriptions of mental activities that typify
mathematical thinking, we would suggest that the solution shows
evidence of sorting, organising, changing and comparing
systematically as well as routine calculating procedures. Solutions
do sometimes offer insights into some of the pre-conceptions that
children might have, although in this case the solution reveals
very limited information along these lines. Our knowledge of
children's experiences of mathematics in school would suggest that
it is likely that the children often expect maths to be a very
compartmentalised subject and involve routine practice of
procedures (Boaler 1997) rather than novel problems. As such this
question would challenge them: they are being expected to think
about and around a mathematical situation rather than practise a
familiar technique. In doing so, they have the opportunity to
extend their knowledge of the connections between different aspects
of mathematical practice. The problem is an elementary one but
links square numbers with ideas about prime numbers as well as a
consideration of addition and so challenges pre-conceptions that
different mathematical ideas can be separated into different
boxes.
From this example we do not have hard evidence that the
children's knowledge or understanding have improved. However we can
suggest that the challenge involved is likely to extend the
boundaries of their knowledge and understanding as well as
connections between different mathematical ideas. This is supported
by our observations of children who work on our problems and who
frequently make comments about how they have gained knowledge and
insight mathematically from their work.
In posting solutions from children we seek to demonstrate the
communicative aspects of mathematics and emphasise the distinction
between solutions and answers: a solution communicates the
mathematics but an answer is the end. The communication of
mathematics is, we believe, an essential part of its purpose: it is
not an isolated activity undertaken by people in corners or dark
alleys or even ivory towers.
Non-standard tasks help to develop this repertoire by
emphasising the need for "thinking around the problem" and sharing
outcomes. In the presentation of the chosen solution we have
deliberately picked one which shows clear reasoning and a
justification for the answer. By having to justify their findings
to an audience the students are encouraged to think about the key
mathematical ideas that underpin their solution and make sure they
are clearly articulated to others. In this way the child is
applying knowledge in new contexts and hence extending their
repertoire of experiences on which to base future work, they are
improving understanding by making connections between the
properties of primes (only one even prime) and the properties of
square numbers. A range of mathematical concepts are being drawn
together to encourage students to make connections and hence
improve their understanding.
We would suggest that non-standard problems are able to
challenge pupils' preconceptions by exposing them to unfamiliar
contexts in which routine procedures will not offer them easy
answers. Instead they are encouraged by the contexts of the
problems to think about what they know mathematically and consider
it in the light of this new problem. In doing so they develop their
ability to make mathematical sense of the problem and so increase
their knowledge and understanding of the related mathematical
ideas, techniques and strategies.
References
Askew, M., M. Brown, et al. (1997). Effective Teachers of
Numeracy. London, School of Education, King's College London:
122.
Boaler, J. (1997). Experiencing School Mathematics: Teaching
styles, sex and setting . Milton Keynes, Open University
Press.
Watson, A. (2002). Exploring example spaces: what are they
like and how do we move around them?
Watson, A. and J. Mason (1998). Questions and Prompts for Mathematical
Thinking . Derby, Association of Teachers of
Mathematics.
