Diamond Collector
Collect as many diamonds as you can by drawing three straight lines.
In the game below, twenty diamonds have been placed on a grid.
You can enter the equations of three straight lines.
Any diamond that lies on one of your lines counts towards your total.
Try to collect as many diamonds as you can!
Once you've had a go at Level 1, you can click on the purple cog to access the Settings menu and try Levels 2 and 3.
Why play this game?
This game provides an engaging context within which to learn about or consolidate understanding of equations of straight lines. Students can begin by identifying some of the lines easily, but there is incentive to learn about 'harder' lines, such as those with fractional gradients.
The different levels of difficulty in the interactivity are designed to encourage students to become more resilient, challenging themselves to keep going and find the best solution they can.
Possible approach
Begin by demonstrating the game to the class:
"On the grid, each cross represents a diamond. You can draw three straight lines, and the object of the game is to collect as many diamonds as you can. Would anyone like to suggest a line we could draw to start off?"
Show students how to input their lines using the gradient and intercept buttons at the bottom of the screen, and choose three lines to input, then click "Get a score" to count up how many diamonds were collected. You then have the option of showing the computer's solution.
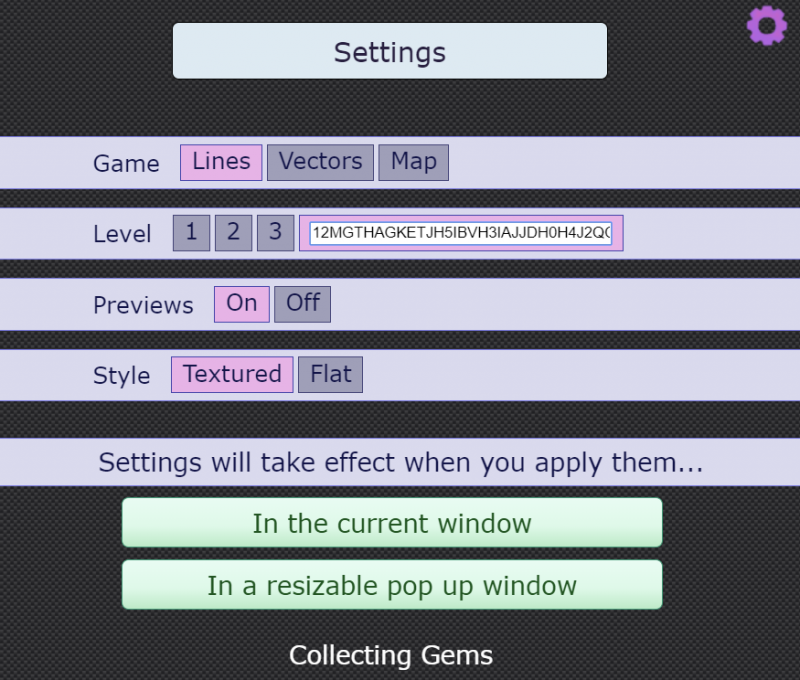
Next, students could work in pairs on computers or tablets. Alternatively, if computers aren't available, there is the option to print out grids. Each distribution of diamonds has a unique code which can be used if you want everyone to work on a particular grid, or if you want to display a particular grid on the board for everyone to see. This can be accessed in the Settings menu - click below for a screenshot.
To access the settings menu, click on the purple cog in the top right corner.
To the right of the Level selectors, there is a code for the current grid.
You will need to click on the box to enter the code, and the border will turn pink as in the screenshot below.
Then click to restart the activity in the current window or in a pop-up window.
In Level 1, the gradient and the intercept have to be whole numbers. In Levels 2 and 3, there is the option to use a fractional gradient and intercept, and the computer will look for solutions that use fractions.
When working in pairs or small groups, insist that students agree with each other about which lines to draw before clicking 'enter' (or before drawing them onto their paper grids). This will encourage them to justify their reasoning and to listen to each others' ideas.
Once students have gained fluency and strategy working in pairs or small groups, you could bring the whole group together to play against the computer. Show a grid to the whole group, and challenge pairs to suggest lines that will collect the most diamonds. You could list suggestions on the board, and then have a whole-group discusion to agree on the best three lines to draw. Can the whole group match the computer?
Key questions
Describe how you move from one diamond to the next in the line you're looking at.
Where would that line meet the y-axis?
Is the slope a positive or a negative gradient? Is it steep or shallow?
Possible support
Possible extension
Challenge students to work on Level 3, with Previews switched off, so that they have to work out the gradients and intercepts without the line being drawn on the screen for them.
