Pole star Sudoku 2
This Sudoku, based on differences. Using the one clue number can you find the solution?
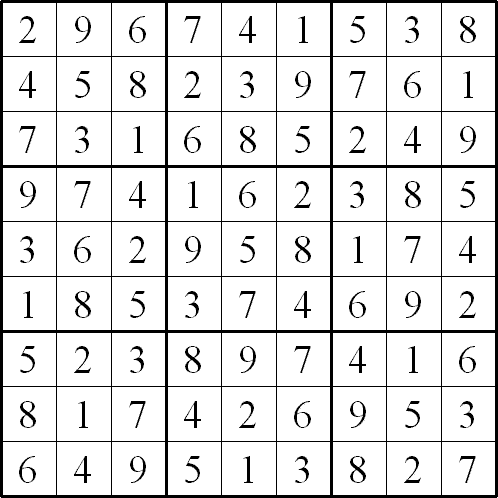
Problem
By Henry Kwok
This Sudoku has a unique solution can you find it?
Image
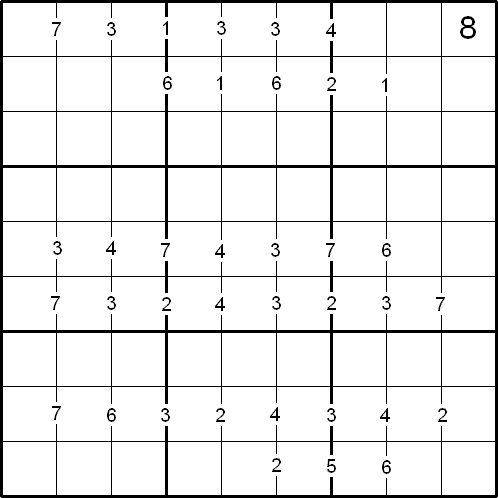
Rules of Difference Sudoku
Like the standard sudoku, the object of the puzzle is to fill in the whole 9x9 grid with numbers 1 through 9 so that each row, each column, and each of the nine 3x3 squares must contain all the nine different numbers.
There are special clue-numbers placed on the border lines between selected pairs of adjacent squares of the grid. Each clue-number is the difference between the two numbers that should be in the respective pair of the adjacent squares just next to left and right from that clue-number.
For example, a clue-number 7 on the border line between two adjacent squares means that possible pairs of numbers for these squares can be from the following combinations: 1 and 8; 2 and 9; 8 and 1; or 9 and 2.
Not much information is there.
However, fortunately for the solver, you can use a starting digit (digit 8 in the top right-hand corner) as the Pole Star to guide you out of the "wilderness" of the puzzle. As this problem is like the Pole Star Sudoku posted on the NRICH site in September 2006, it is called Pole Star Sudoku 2.
Student Solutions
Image