Presents
Problem
It's often time to be giving presents to friends. We usually wrap them up so that there is some fun in unwrapping them. Little baby brothers and sisters tend to like the unwrapping more than the present itself!
We should probably try to save paper, though, and use no more than is necessary. So let's do some wrapping up and never have one piece of paper overlapping another. Remembering this, let's have a look at a very practical challenge.
It would probably be good to use some of those cubes which fit together [multilink] that are around in most schools and put perhaps 27 of these together to make a cube [which in this case would be 3 by 3 by 3].

This is just so that we can have a reasonable sized prezzie, maybe it's a box with an interesting game in it ... I don't know!
We are just concerned with its shape:-

We need to wrap it up, remembering that we can have no overlaps. One rule here is that the paper will be made up of squares the size of the faces of the cube.
So you may decide on something like this:-
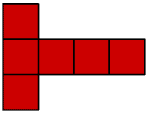
You notice that I've used red paper that is red on both sides so that nothing changes if I turn it over.
You could of course find other shapes to use. Here are just two more:-

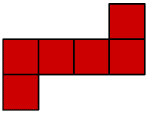
Now you find the rest!
Remember to avoid reflections or turning over!
Now for part two of this challenge. What happens if we make one of the sides of this cube a bit different so that it becomes a cuboid?

How many different shapes of paper can be used this time?
Try to find them all.
Now for the third part. What if the prezzie were different from a cube in two directions?

Can you predict how many different shapes of wrapping paper there will be this time?
If you can't, then make them all - that's one sure way of finding out!
Well, good luck with this rather different challenge which only becomes an investigation when you now ask the question "I wonder what would happen if ...?''
Getting Started
You could always start the other way around - with the wrapped cube - and find different ways of cutting the paper off, remembering to keep the pieces covering each face as a square.
Can you try to visualise wrapping the present in different ways and then try to draw the shape of paper you needed?
Student Solutions
No one has sent in a complete solution for this problem, so please send one in if you think you have it. These two partial solutions from Joanne and Jill might get you thinking!!
Joanne, West Flegg Middle School says:
I first took your plans and developed them.
After that I thought about what didn't work in the patterns and I found that groups of 4 squares together in a square didn't work:
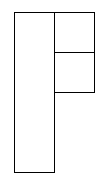

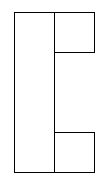
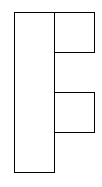
These shapes do not work
These shapes do work. They are nets of a cube:
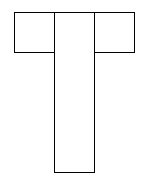
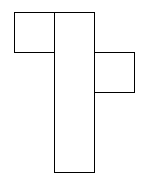
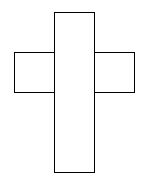
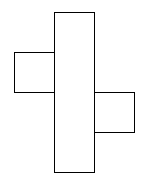
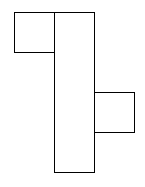
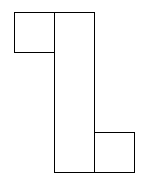
I think there are 6 different ways of covering this parcel.
Task 2: To make a net for a cuboid.
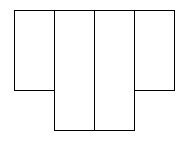
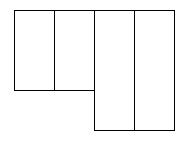
These did not work.
I found that you could not have the 2 end squares on the same side.
These are the nets that did work:
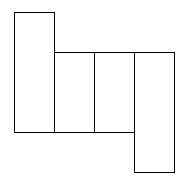
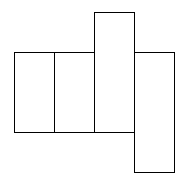
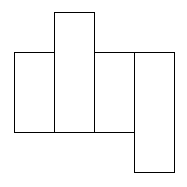
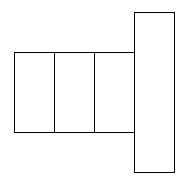
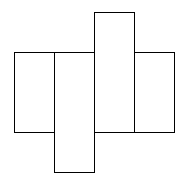
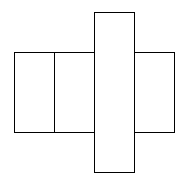
I found 6 nets that will cover this parcel.
I predict that for the present that is different from a cube in 2 directions the number of nets is 3.
Jill, also from West Flegg Middle School, says:
First of all I found several different ways of the non net (reflected, upside down, sideways). Here are two that I found the most:
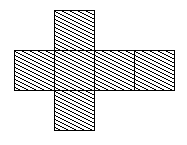
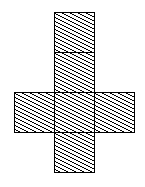
But then, when cutting out the card to test it, I cut it
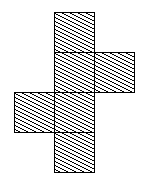
wrongly.![]()

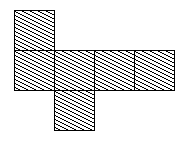
But then, when I came to this one which didn't work, I realised something: the squares that are moved have to be on the same side.
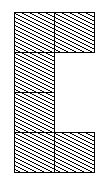
This led to some interesting thoughts:
- How many other nets can be made?
- What would happen if there weren't two squares on different
sides?
- Can we do this with other 3D shapes?
Well, the truth is there must be answers out there somewhere.
Teachers' Resources
Why do this problem?
This activity is very good for introducing the concept of surface area. Being very practical it helps pupils to understand the ideas before looking at any kind of formulae. It also widens the pupils' experiences of nets.
Possible approach
Key questions
Have you checked to see if your paper shape works? (it's good to ask this even when you can see it's a good one!)
