Common Tangent
Two circles touch, what is the length of the line that is a tangent to both circles?
Problem
Two circles with radii 1cm and 4cm touch. The point P is on the smaller circle, Q is on the larger circle, and PQ is a tangent to both circles. What is the length of PQ?
Image
Student Solutions
The diagram shows points A and B, the centres of the two circles, and C, on line BQ such that AC is parallel to PQ. Since ACQP is a rectangle, ACB is a right angled triangle. So By Pythagoras' Theorem, AC=4, which is also the length of PQ.
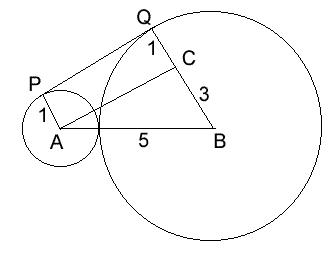
Image

