Blockupied
A 1x2x3 block is placed on an 8x8 board and rolled several times.... How many squares has it occupied altogether?
Problem
Image
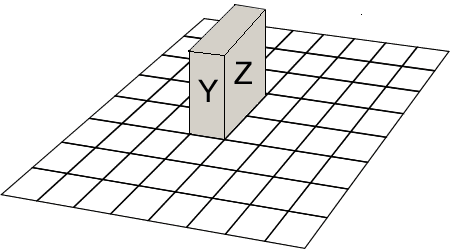
A $1\times2\times3$ block is placed on an $8\times8$ board, as shown with the $1\times2$ face $X$ at the bottom.
It is rolled over an edge, without slipping, onto a $1\times3$ face $Y$, then onto the $2\times3$ face $Z$, then onto $X$, $Y$, $Z$ again in that order.
How many different squares on the board has the block occupied altogether, including the starting and ending positions?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Image
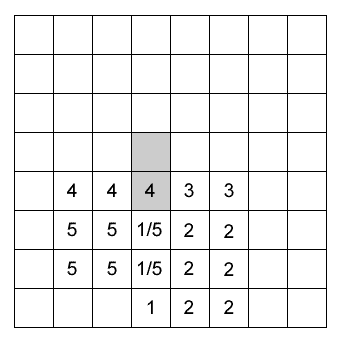
The two shaded squares are those on which the block began.
After the first move, it occupies the squares labelled $1$ (or $1/5$).
After the second move, it occupies the squares labelled $2$ and so on.
After the fifth and final move, it occupies the squares labelled $5$ (or $1/5$).
By the end, $19$ squares will have been occupied altogether.
