Two Number Lines
Max and Mandy put their number lines together to make a graph. How
far had each of them moved along and up from 0 to get the counter
to the place marked?
Problem
You could try Number Lines before this problem.
Max and Mandy both had number lines. Max's number line went along from left to right like this:
Image
Mandy's number line went up and down like this:
Image
Max and Mandy both started at zero on their number lines. Max made a secret jump along his number line and then moved on seven and landed on $10$. How long was his secret jump?
Mandy made a jump of three and another secret jump. She landed on $6$. How long was her secret jump?
Max and Mandy decided to put their number lines together. Their teacher gave them some squared paper. They had made a graph. It looked like a bit like this:
Image
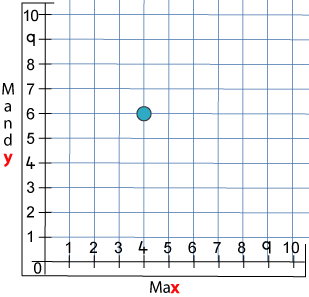
Max moved four along and Mandy moved six up. They put a counter on the place they landed. Now their graph looked like this:
Image
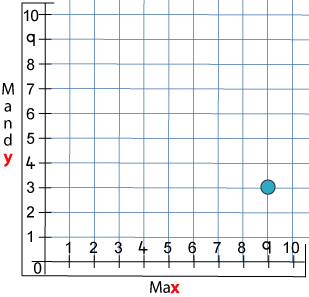
How far had each of them moved along and up from $0$ to get the counter to the place marked on the grid below?
Image
If Max and Mandy both moved the same distance along and up, where could the counter be?
Getting Started
It might help to have some number lines to draw in the jumps. You could print off these pages of number lines.
If they both moved the same distance along or up their number line, can you think of a number of jumps they could have made? You could mark that on a graph of your own.
What about a different number of jumps? And a different number again?
Student Solutions
We had particularly good solutions from Callum at St Patrick's School, Boyang from Mountfields Lodge and Caroline from St Jude's C of E School. Caroline wrote:
Max's secret jump was 3, 10-7=3Mandy's secret jump was 3, 6-3=3
On the grid, Max had moved 9 along and Mandy had moved 3 up.
She goes on to say:
If Max and Mandy both move the same distance along and up, the counter could be at:0 along and 0 up
1 along and 1 up
2 along and 2 up
3 along and 3 up
4 along and 4 up
5 along and 5 up
6 along and 6 up
7 along and 7 up
8 along and 8 up
9 along and 9 up
10 along and 10 up
This line is a diagonal line.
That's right! Boyang and Callum gave the coordinates of the points. Callum said:
(0,0) or (1,1) or (2,2) or (3,3) or (4,4) or (5,5) or (6,6) or (7,7) or (8,8) or (9,9) and could go on forever.Teachers' Resources
Why do this problem?
This problem follows on from Number Lines and could be used to introduce coordinates. In addition to focusing on ideas associated with inverse operations and algebra, the final part of this activity asks pupils to find all possibilities, giving them an opportunity to identify and explain
the pattern produced on the graph.
Possible approach
It would be good for learners to work on this task practically, with number lines, squared paper and counters. These sheets of number lines could be printed off and cut out for this purpose.
Key questions
How far up Mandy's number line has the counter been put?
How far along Max's number line has the counter been put?
Where are you going to put your counter now?
If they both moved the same distance along or up their number line, can you think of a number of jumps they could have made?
What about a different number of jumps?
Can you think of a word to describe that line?
