Inside Triangles
Problem
Here is a four by four dotty grid:
I have joined three dots on the grid to make a triangle which has one dot inside it:
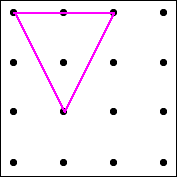
How many different triangles with one dot in the middle can you draw?
How do you know have found them all?
You may like to experiment with the pegboard interactivity below, or you could print off this page of dotty grids to work on.
Getting Started
You might want to work with a partner so you have someone to check that your triangles are all different.
Have you got all the triangles which have a corner at the corner of the grid?
Student Solutions
Shree from the International School Frankfurt in Germany sent in these solutions in which triangles in different places were explored:
Neptune Class from Riverley Primary wrote to say:
We think that there are 6 triangles in total.
We made sure that each triangle was a different type (scalene, isosceles, right-angled and equilateral) and we experimented with different shapes on the pin-board.
We thought that there must also be a mathematical way to systematically calculate the solution to the problem, but we're still working on it.
I think there are a few more than six triangles, but I like the way you thought that working systematically would help.
That's exactly what Greg from Swanland County Primary School did. He said:
First I tried to just make triangles with a dot inside.
Then I tried ones with a four dot base.
Then I tried one with a two dot base.
I think there are 7 different triangles.
These show some very good approaches. Thank you for sending them into us.
Some of you might like to explore further, being curious about what having two dots within the triangles would be like, for example.
Teachers' Resources
Inside Triangles
Here is a four by four dotty grid:
I have joined three dots on the grid to make a triangle which has one dot inside it:
How many different triangles with one dot in the middle can you draw?
How do you know have found them all?
You may like to experiment with the pegboard interactivity below, or you could print off this page of dotty grids to work on.
Why do this problem?
This low threshold high ceiling activity is accessible to all pupils but has the scope to be extended in many directions. In order to make a start, children will need to be familiar with properties of triangles, but drawing triangles on the grid will help them to clarify for themselves what they understand by the term "triangle". In order to find all the possible triangles, pupils will need to work in a systematic way.
Possible approach
You may want to begin this task with the whole class and, this way, the notion of "different" will come up quite quickly. How is the group going to define "different"? This is a great discussion point and one where there isn't a right or a wrong answer. You could decide to count triangles which could be picked up and placed exactly on top of another triangle as the same. Or, you could decide that they are different if they are in a different orientation on the grid. The former suggestion makes a more manageable number to count!
Key questions
Tell me about the way you're working.
How will you remember which triangles you've found?
How do you know that your triangles are all different from each other?
How do you know that you have found them all?
Possible support
Having a range of different equipment available for children to use to tackle this problem (e.g. pegboards, grids on paper, the interactivity) will help everyone get started.
If learners are finding it difficult to work systematically, you could offer them 6 Beads and Three Ball Line Up first, which might be a more familiar context.
Possible extension
In order to extend the problem, pupils could be asked to find triangles with three spots inside them or no spots inside... Differently sized grids could be drawn and compared. You could sort the triangles across differently sized grids, for example all right-angled triangles together, or all triangles which are the same shape but different sizes together.