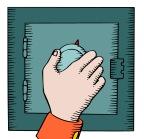
How Safe Are You?
How much do you have to turn these dials by in order to unlock the safes?
Problem
We're going to look at opening safes!
Many have dials on them, and you turn the dials to open them, like in the picture below.

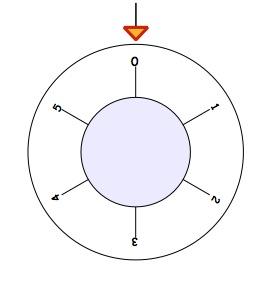
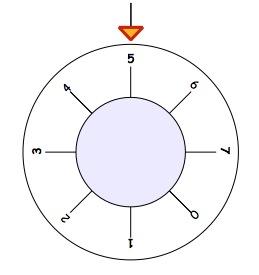
To open the safe, the dial has to be turned so that the number $2$ is next to the arrow, like this:
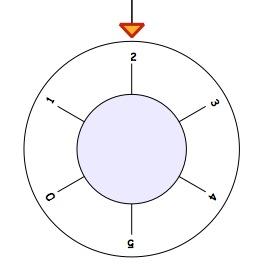
How much was the dial turned to get the $2$ at the top?
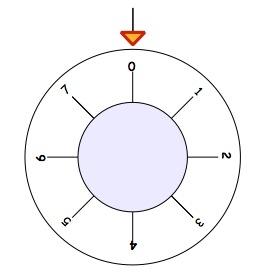
The safe below has a different dial with the numbers $0 - 7$ instead.
How much does the dial have to be turned to get between these two pictures, so that the number $5$ is at the top?
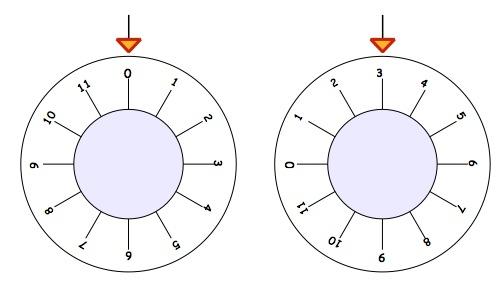
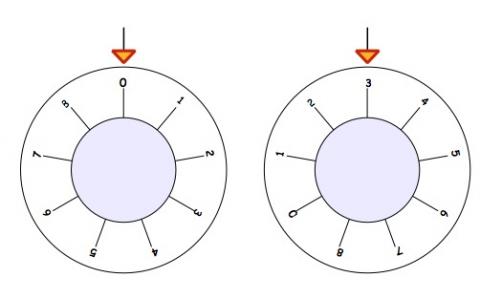
The number that you have to get at the top is often called the "combination" of the safe. These three different safes all start with $0$ at the top. You have to find the amount of turning to get to the combination, shown in each second picture:
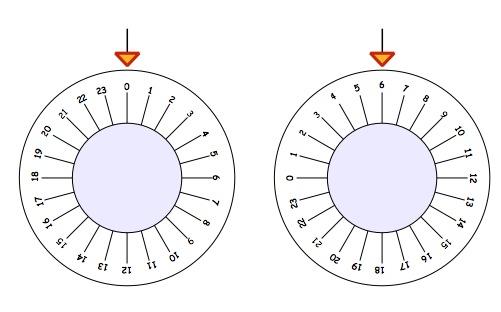
Now have a go at these different safes. Remember they would all start with $0$ at the top. How much does each one need to be turned to get to the combinations shown below?
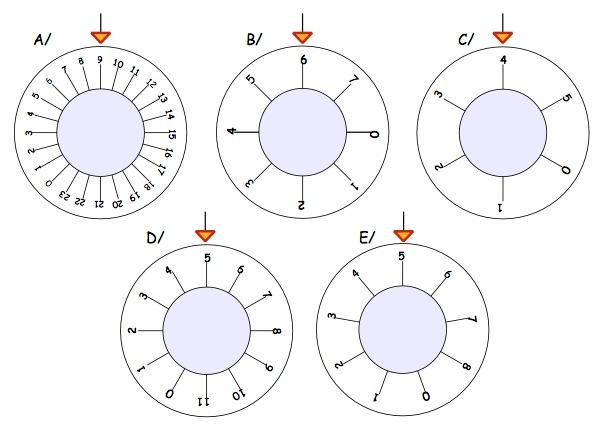
5 dials labelled A to E. Dial A has numbers from 0 to 23 and an arrow pointing to 9. Dial B has numbers 0 to 6 around the outside and an arrow pointing to 6. Arrow C has the numbers from 0 to 5 around the outside and an arrow pointing to 4. Dial D has the numbers 0 to 11 around the outside with an arrow pointing to 5. Dial E has the numbers 0 to 8 around the outside with an arrow pointing to 5.
Getting Started
Does it matter in which direction we turn the dial?
Is it more than half a full turn each time? Can you be more exact?
Perhaps you know how many degrees there are in a circle?
Student Solutions
George and Dominic from St Nicolas C of E Junior School sent us very clearly explained solutions to this problem. Thank you! Here is what they wrote for the first part:
George and Dominic continued to explain how they had gone about the second part of the solution:
Very well done to you both. You obviously worked hard on this activity. Thank you too, to Eve and Rachel from Castle Carrock Primary who also sent in well-explained solutions.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
A circular protractor would be useful for some pupils. Some preliminary discussion could be had about the turning involved in an analogue clock.