Four Go
This challenge is a game for two players. Choose two of the numbers to multiply or divide, then mark your answer on the number line. Can you get four in a row?
Problem
Draw a number line on a piece of paper, marked from $0$ to $20$, like this:

(You could print off this sheet of number lines.)
This challenge is a game for two players. The first player chooses two numbers in this grid and either multiplies or divides them.
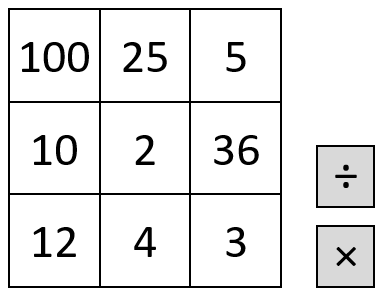
They then mark the answer to the calculation on the number line. The second player then chooses two numbers and either $\times$ or $\div$, and marks that number in a different colour on the number line.
If the answer is too big or too small to be marked on the number line, the player misses a go.
The winner is the player to get four marks in a row with none of their opponent's marks in between.
What good ways do you have of winning the game?
Does it matter if you go first or second?
[This game is adapted from a SMILE Centre card.]
Getting Started
Where on the number line do you want to put a mark? How will you make that answer from the numbers in the grid?
You could use a calculator to check your answers if your opponent doesn't agree!
How will you stop your opponent from getting four in a line before you?
Are there any good places on the number line to start? Are there some places which might not be so good to start? Why?
Student Solutions
Abigail and Amber from Harrison Primary School wrote this very comprehensive reply;
We first started to think about what numbers could and couldn't be made with the digits and operations given. We took out all of the prime numbers (momentarily) as we know that they have no factors (2, 3, 5, 7, 11, 13, 17). However as some of those numbers could be made by multiplying two other numbers together we re-added some of them in (2, 3, 5). Then we found 4 numbers in row that could be made and went for them for the highest chance of winning.
In our opinion we think it doesn't matter if you go first or second (as they both have their advantages). We thought about it logically and found all easy possibilities of a sequence of 4 in a row. To do this we took out prime numbers that had no factors and couldn't be made by multiplying 2 numbers together then we looked at 4 numbers in a row that could be made.
Now we looked at would it matter if you went 1st or second? As we started to dig deeper we realize that they both had their pros and cons. When you went first you had the choice of picking what row you wanted to go for, however then the other person could see what angle you were going for and block you immediately. Then its was the same for going 2nd, you could easily block your opponent yet they got the first choice of their 4 in the row sequence.
Arti wrote to us to say:
There are two things that are not defined which need a definition:
- If player A marked a number in the number line, can player B mark it later?
- If player A used two numbers from the square, can player B use one or both those numbers?
These are good questions, Arti. What did you decide in the game/s you played? Did that work well? You could try out both versions and decide which works better.
Rowena from Christ Church Primary told us:
I played this game with my Mum and neither of us won. We played it again and my Mum let me win!
We decided to list all the possible whole number answers. They were 2, 3, 4, 5, 6, 8, 9, 10, 12, 15 and 20. Once we knew these, it was easy to choose numbers to block the opponent and not let them get four in a row.
You can only win if your opponent makes a mistake or lets you win!
Thank you, Rowena - that was a good idea to make a list of the whole number answers.
I wonder whether you could change the game to make it a better game?
Teachers' Resources
Why do this problem?
This game gives children the opportunity to estimate answers to calculations in a motivating context, and gives plenty of practice in multiplication and division. Playing strategically involves higher-order thinking and the need to think ahead.
Possible approach
You could play the game on the board against another adult (or a child who has been told the rules), but without saying anything about the rules to the whole group. You could write down each calculation as you go along. Invite the class to watch the game in action and after a few moves, ask them to suggest what they think the rules might be. How might the game be won? Having discussed the possibilities as a whole class, explain the rules as described in the problem itself and set the children off playing in pairs on some number lines.
