Quaternions and rotations
Find out how the quaternion function G(v) = qvq^-1 gives a simple
algebraic method for working with rotations in 3-space.
Problem
Image

|
In this question we see how quaternions are used to give rotations of ${\bf R^3}$. |
Image
|
(1) Consider the quaternion $$q = {1\over \sqrt 2} + {1\over
\sqrt 2}{\bf i} + 0{\bf j} + 0 {\bf k}.$$ (a) Show that the
multiplicative inverse of $q$ is given by $$q^{-1} = {1\over \sqrt
2} - {1\over \sqrt 2}{\bf i}$$ (b) Show that for all scalar
multiples $x = t{\bf i}$ of the vector ${\bf i}$, $q x = x q$ and
hence $q x q^{-1} = x$. This proves that the map $F(x) = q x
q^{-1}$ fixes every point on the x axis.
(c) What happens to points on the y axis under the mapping
$F$? To answer this work out $F({\bf j})$. Also compute $F({\bf
k})$ and show that ${\bf k} \to {\bf -j}.$
|
|
(2) Consider the quaternion $q = \cos \theta + \sin \theta
{\bf k}$
(a) Show that $\cos \theta - \sin \theta {\bf k}$ is the
multiplicative inverse of $q$.
(b) Show that $q{\bf k}q^{-1}={\bf k}$.
(c) Show that $$q v q^{-1}= r(\cos (2\theta + \phi) {\bf i} +
\sin (2\theta + \phi){\bf j})$$ where $v = (r\cos \phi {\bf i} +
\sin \phi {\bf j}+0{\bf k})$ and hence that the map $G(v)= q v
q^{-1}$ is a rotation about the z axis by an angle $2\theta$.
|
Image
|
To read about number systems,
where quaternions fit in, why there are no three dimensional
numbers and numbers in higher dimensions, see the NRICH article
What
Are Numbers?
If you want to know how
quaternions are used in computer graphics and animation in film
making read the Plus Article Maths
goes to the movies .
The NRICH article The use of
maths in computer games tells you a lot more about the subject.
Though this article uses complex numbers and vectors and not
quaternions,the mathematics is the same with quaternions which just
give a shorter and neater way of writing down and working with the
functions that give reflections and rotations in 3-space
.
Student Solutions
Andrei from Romania sent in a good solution to this problem.
(1)(a) We have to show that $qq^{-1} = 1$: $$q^{-1} = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i}) = {1\over 2}(1 - {\bf i}^2) = 1$$ (b)Take $x = ti$ to be any point on the x-axis. Then $qx = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t{\bf i} = {-1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t = xq.$
We have shown that $qx = xq$ and so $qxq^{-1} = x$.
Image
|
Let $F(v) = qvq^{-1}$ be a mapping of points $v$ in $R^3$ to images in $R^3$ where the 4-dimensional quaternion $q$ acts as an operator. We have proved that this mapping fixes every point on the x axis. |
(c)What effect does this mapping have on other points in
$R^3$? $$F({\bf j})= qjq^{-1} = ({1\over \sqrt 2} + {1\over \sqrt
2}{\bf i})({\bf j}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i})$$
$$ = {1\over 2}(1+{\bf i})({\bf j})((1 - {\bf i})$$ $$ = {1\over
2}({\bf j} + {\bf k})(1 - {\bf i})$$ $$ = {1\over 2}({\bf j} + {\bf
k} + {\bf k} - {\bf j})$$ $$= {\bf k}.$$ Similarly $F{\bf k} =
-{\bf j}$. Parts (b) and (c) together show that the mapping $F(v) =
qvq^{-1}$, where $q = \cos (\pi /4) + \sin (\pi /4) {\bf i}$, gives
a rotation of $\pi /2$ about the x axis.
Image
|
(2) In this section we consider the mapping $G(v) = qvq^{-1}$ of $R^3$ to $R^3$ where the quaternion $q = \cos \theta + \sin \theta {\bf k}$ is an operator. |
(a) $(cos \theta + \sin\theta k)(\cos \theta - \sin \theta k)
= \cos^2 \theta + \sin^2 \theta = 1$ so these two quaternions are
multiplicative inverses.
(b) We have $qk = -\sin \theta + \cos \theta k = kq$ and hence
$qkq^{-1} = k$. So the mapping $G(v) = qvq^{-1}$ fixes the
z-axis.
(c) What effect does the mapping $G$ have on vectors in $R^3$?
We consider the vector $v = r(\cos \phi {\bf i} + \sin \phi {\bf
j})$. $$ qvq^{-1} =(\cos \theta + \sin \theta {\bf k})r(\cos \phi
{\bf i} + \sin \phi {\bf j}) (\cos \theta - \sin \theta {\bf k}) $$
$$= r((\cos \theta\cos \phi - \sin \theta \sin \phi){\bf i} +(\cos
\theta \sin \phi + \sin \theta \cos \phi){\bf j}) \cos \theta {\bf
i} -\sin \theta {\bf k}) $$ $$ = r(\cos (\theta + \phi) {\bf i} +
\sin (\theta + \phi){\bf j}) (\cos \theta {\bf i} -\sin \theta {\bf
k}) $$ $$= r((\cos (\theta +\phi)\cos \theta - \sin (\theta +
\phi)\sin \phi){\bf i} + (\cos (\theta +\phi)\sin \theta + \sin
(\theta + \phi)\cos phi){\bf j})$$ $$= r(\cos (2\theta + \phi){\bf
i} + \sin (2\theta + \phi){\bf j}).$$
Image
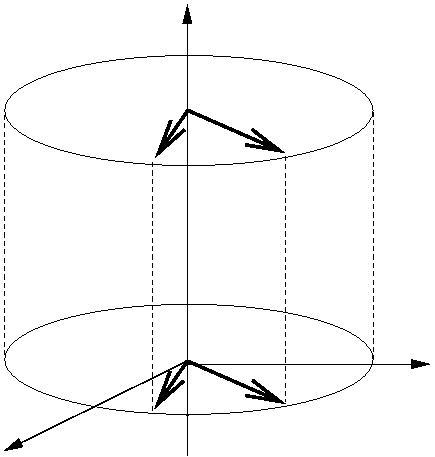
|
We have shown $qkq^{-1} = k$ so $G(v+tk)= q(v +tk)q^{-1} =
qvq^{-1} + qtkq^{-1} = qvq^{-1} + tk$ for all $t$.
We can see that the vector $v$ in the $xy$ plane is rotated
about the $z$ axis by an angle $2\theta$ and all points on the vertical line through
it are also rotated about the $z$-axis by an angle
$2\theta$.
So by the mapping $G(v) = qvq^{-1}$ all points in $R^3$ are
rotated by $2\theta$ about the $z$-axis.
Note that, for any rotation of $R^3$, we can make a
transformation of the coordinate system so that the axis of the
rotation is made to coincide with the $z$-axis, then perform the
rotation by the given angle about the $z$-axis, and finally
transform back to the original coordinate system.
|
Teachers' Resources
Comparing the results in parts (1) and (2) we see that in part (1)
$q = \cos 45^o + \sin 45^o{\bf i}$ and the map $qvq^{-1}$ fixes the
x-axis and gives a rotation of twice 45 degrees about the x-axis.
The result in (2) is slightly more general showing that where $q = \cos \theta + \sin \theta {\bf k}$ the map $q v q^{-1}$ fixes the z-axis and gives a rotation of $2\theta$ about the z-axis. \par For a more general account of quaternions and rotations see the article....
The result in (2) is slightly more general showing that where $q = \cos \theta + \sin \theta {\bf k}$ the map $q v q^{-1}$ fixes the z-axis and gives a rotation of $2\theta$ about the z-axis. \par For a more general account of quaternions and rotations see the article....
